Пол Прюсс - Венера Прайм 2

Париж. Вокзал Сен-Лазар.

Мальстрим — водоворот в Норвежском море у северо-западного побережья Норвегии.

Математика описываемого полета :

Скорость убегания для Луны (2-я космическая скорость), скорость позволяющая телу покинуть сферу ее притяжения составляет 2380 метров в секунду (8568 км\час). В нашем случае разгон происходит с ускорением 8g, где g — ускорение свободного падения на поверхности Земли (g = 9,77 м\сек 2, примерно 9,8) за 31 секунду. Следовательно шаттл разгоняется до скорости 2423 метров в секунду (8 х 9,77 х 31), то есть скорость даже больше минимально необходимой. Нетрудно подсчитать, что длина разгона составит 37,6 км (в главе первой третьей части длина разгонной эстакады — более 40 км). Упоминание g дано в данном случае для наглядности, например при старте современных космических кораблей космонавты испытывают ускорение 7g.

Математика описываемого полета (продолжение):

Масса Луны. М = 7,5 х 10 22кг

Гравитационная постоянная. G = 6,67 : 10 11м 3/кгс 2

Радиус Луны. r = 1,75 х 10 6м (1750 км)

Расстояние от центра Луны до точки, в которой герой совершает прыжок из шаттла, апогей орбиты. R = 3,16 х 10 7 м (31600 км) — в тексте: «до Луны было, как ему сказали, около тридцати тысяч километров», (29850 + 1750 = 31600).

Скорость движения шаттла по орбите вычисляем из формулы:

V 2= 2GМ(1/r — 1/R), получаем V = 2324 м/с или 8366 км/час.

Скорость убегания 8568 км\час.

8568 — 8366 = 202 км\час — в тексте : «Переключатели одной секции катапульты по непонятной причине не сработали, и твоя скорость меньше нужной на двести километров».

Большая ось эллипса орбиты — R + r = 33350 км. Для простоты длину орбиты посчитаем как длину окружности диаметром 33350 км, тогда время оборота найдется:

T = 3,14 х 33350 : 8366; T = 12,5 часа — в тексте: «то закончив оборот, примерно через десть часов, ты окажешься там откуда начал». — Возможно верно ведь орбита все-таки эллипс, а не окружность.

И теперь самое главное. Определим на сколько герою удалось повысит свою орбиту.

Прыжок происходит из точки апогея, расстояние до центра Луны (максимальное) — R = 3,16 х 10 7 м.

Вычисляем ускорение свободного падения Луны на такой высоте по формуле:

g = G х М : R 2, получаем g = 0,005 м/с 2, то есть ускорение там в 2000 раз меньше, чем на Земле. По сути описывается прыжок с места в высоту. И если на Земле герою удалось бы заскочить на уступ примерно в метр высотой, то в описываемой ситуации в 2000 раз выше, но ему вряд ли удалось бы повысить высоту орбиты более чем на 1000 м, поскольку вес скафандра, да и не удобно в нем прыгать. На такой высоте он должен, по идее, пролететь над поверхностью, над разгонной катапультой.

Что касается времени, то расчеты показывают, что шаттл прилетел бы всего лишь на какие-то десятые дли секунды раньше человека.

Возможно, нижеприведенная схема облегчит понимание словесного описания этого полета:

«А в иллюминаторе красовалась Земля. Она была почти полной, в три четверти, и такой яркой, что просто ослепляла.» — Шаттл находится в точке О 1 и дуга 1-2 действительно примерно три четвертых диаметра.

«Клифф мчался, приближаясь к ночной стороне Луны, и ее полумесяц (освещенная Солнцем часть) постепенно уменьшался.» — Герой в точке О 2и серп Луны это дуга 4-5. Линия З-4 разделяет Луну на дневную и ночную половины.

«Когда он проснулся, Солнца видно не было — полет происходил в тени Луны.» — Дуга О 3-О 4.

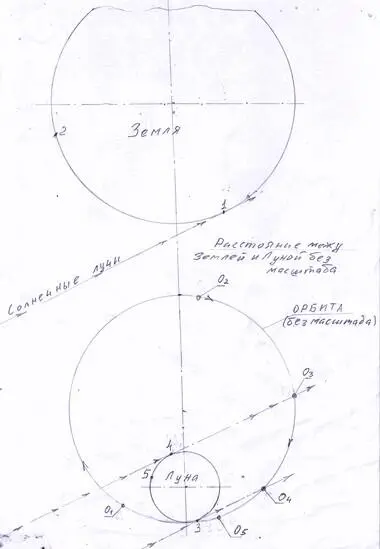
«Возможно, он в последний раз видит родную планету…» — Герой приближается к точке О 5, после ее прохождения Луна закроет Землю (освещенную току 1).

Жозеф Луи де Лагранж (1736-1813) — французский астроном и математик, ввел в астрономию понятие «точки Лагранжа».