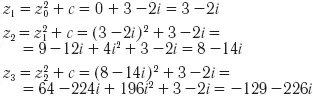Максим Кидрук - Бот

Комплексные числа можно представить геометрически (визуально). Возьмем площадь с прямоугольной (декартовой) системой координат. На оси абсцисс будем откладывать значения x , на оси ординат — y (см. рис. ниже). А любое комплексное число ( z 0= x 0+ iy 0или z 1= x 1+ iy 1) можно изобразить как точку на этой плоскости (соответственно с координатами { x 0, y 0} и { x 1, y 1}). Эта плоскость получила название комплексной .

N. B. Обратите внимание: действительные числа (те, которыми мы пользуемся в быту) на комплексной площади соответствуют исключительно оси абсцисс. Для них y = 0 . Введение понятия комплексных чисел невероятно расширило границы математических вычислений. Это как будто другая реальность, новое измерение. На комплексной площади эти числа — все, что лежит выше и ниже оси абсцисс. Другими словами, с точки зрения математики действительные (обычные) числа — это скорее исключение. Преимущественное большинство значений выражается именно комплексными, а не действительными числами.

Геометрическое представление комплексных чисел на комплексной площади

Вот теперь мы наконец подошли вплотную к множеству Мандельброта.

Математик Бенуа Мандельброт исследовал так называемые рекурсивные последовательности: каждое следующее значение z такой последовательности получалось из предыдущего по формуле: z i +1= z i 2+ c , где с — произвольное комплексное число.

Возьмем для примера c = 3 –2 i.

Тогда первые три члена последовательности будут равняться:

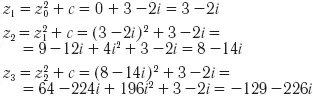
и так далее…

Что же там исследовать, спросите вы? Да почти ничего. Каждое из новых полученных z i также является комплексным числом и, соответственно, обозначается такой точкой на комплексной площади. Математики еще задолго до Мандельброта заметили, что некоторые z i стремятся к бесконечности, а другие — группируются, то есть направляются к какому-то конкретному числу. Такое странное поведение не подчинялось никаким теориям, аналитически его не смогли объяснить. Ученых заинтересовало, какую геометрическую фигуру образует эта совокупность точек последовательности z i +1= z i 2+ c . Круг? Эллипс? Возможно, хаотический набор точек? Какой-нибудь сложный рисунок?

До появления ЭВМ определить это не удавалось. Бенуа Мандельброт первым применил ЭВМ и графическую систему для решения такой задачи. К последовательности z → z 2+ c Мандельброта подтолкнули длительные раздумья о разительном сходстве при рассматривании береговой линии, горного рельефа и других природных объектов в разных масштабах .

Также Мандельброт взялся за построение. Если точка не стремилась к бесконечности, компьютер изображал ее черным цветом на комплексной площади. В другом случае точка оставалась белой.

К своему удивлению, Мандельброт получил фигуру, напоминающую кардиоиду с многочисленными присоединенными к ней овалами. Он не ожидал, что простая на вид формула может дать настолько сложное изображение. Но главное удивление ожидало его впереди.

Множество Мандельброта на комплексной плоскости

Мандельброт выбрал часть изображения и увеличил ее, подбирая начальные точки z 0с большой точностью. Открывшаяся картина поразила его. То, что на большом изображении казалось точкой или невыразительным пятном, при увеличении оказалось удивительным узором, в котором то тут, то там попадалась точная копия главного изображения — фантастической кардиоиды. Дальнейшие увеличения открывали перед Бенуа еще более невероятные узоры, все части которых были соединены между собой. При данном увеличении математик видел точку. Но стоило углубиться, как эта точка превращалась в фантастически закрученные галактики.

Мандельброт не мог поверить в то, что видит. Рисунок был плоским, но математик углублялся в него, как будто тот был трехмерным. Это все равно что заглянуть в собственный шкаф с одеждой и вдруг обнаружить за ним портал, ведущий на другую планету, ландшафты которой настолько прекрасны, что просто нельзя описать словами. Это не укладывалось в голове. Такого не могло быть! Невиданная безграничность форм и образов просто не могла прятаться в настолько простой, банальной алгебраической формуле. Но это еще не все.