Arthur Clarke - The Ghost from the Grand Banks

Emerson laughed. “I wouldn’t be surprised. And he’ll he asked to repeat the act, every time he goes on TV.”

He thought it unnecessary to add that, besides his many other talents, Parkinson was quite a good amateur conjurer. Even with freeze-frame, no one would be able to spot what had really happened to that pill.

And there was another reason why he preferred not to join the panel—he was an outsider, and this was a family affair.

Though they lay centuries apart, Mary Rose and Titanic had much in common. Both were spectacular triumphs of British shipbuilding genius—sunk by equally spectacular examples of British incompetence.

It was hard to believe, Jason Bradley told himself, that people actually lived like this, only a few generations ago. Though Conroy Castle was a very modest example of its species, its scale was still impressive to anyone who had spent most of his life in cluttered offices, motel rooms, ships” cabins—not to mention deep-diving minisubs, so cramped that the personal hygiene of your companions was a matter of crucial importance.

The dining room, with its ornately carved ceiling and enormous wall mirrors, could comfortably seat at least fifty people. Donald Craig felt it necessary to explain the little four-place table that looked lost and lonely at its center.

“We’ve not had time to buy proper furniture. The castle’s own stuff was in terrible shape—most of it had to be burned. And we’ve been too busy to do much entertaining. But one day, when we’ve finally established ourselves as the local nobility…”

Edith did not seem to approve of her husband’s flippancy, and once again Bradley had the impression that she was the leader in this enterprise, with Donald a reluctant—or at best passive—accomplice. He could guess the scenario: people with enough money to squander on expensive toys often discovered that they would have been happier without them. And Conroy Castle—with all its surrounding acres and maintenance staff—must be a very expensive toy indeed.

When the servants (servants!—that was another novelty) had cleared the remnants of an excellent Chinese dinner flown in especially from Dublin, Bradley and his hosts retreated to a set of comfortable armchairs in the adjoining room.

“We won’t let you get away,” said Donald, “without giving you our Child’s Guide to the M-Set. Edith can spot a Mandel-virgin at a hundred meters.”

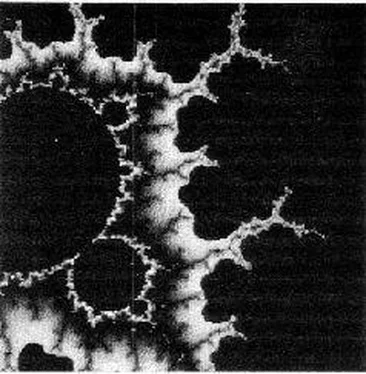
Bradley was not sure if he qualified for this description. He had finally recognized the odd shape of the lake, though he had forgotten its technical name until reminded of it. In the last decade of the century, it had been impossible to escape from manifestations of the Mandelbrot Set—they were appearing all the time on video displays, wallpaper, fabrics, and virtually every type of design. Bradley recalled that someone had coined the word “Mandelmania” to describe the more acute symptoms; he had begun to suspect that it might be applicable to this odd household. But he was quite prepared to sit with polite interest through whatever lecture or demonstration his hosts had in store for him.

He realized that they too were being polite, in their own way. They were anxious to have his decision, and he was equally anxious to give it.

He only hoped that the call he was expecting would come through before he left the castle…

Bradley had never met the traditional stage mother, but he had seen her in movies like—what was that old one called?—ah, Fame. Here was the same passionate determination on the part of a parent for a child to become a star, even if there was no discernible talent. In this case, he did not doubt that the faith was fully justified.

“Before Ada begins,” said Edith, “I’d like to make a few points. The M-Set is the most complex entity in the whole of mathematics—yet it doesn’t involve anything more advanced than addition and multiplication—not even subtraction or division! That’s why many people with a good knowledge of math have difficulty in grasping it. They simply can’t believe that something with too much detail to be explored before the end of the Universe can be generated without using logs or trig functions or higher transcendentals. It doesn’t seem reasonable that it’s all done merely by adding numbers together.”

“Doesn’t seem reasonable to me, either. If it’s so simple, why didn’t anyone discover it centuries ago?”

“Very good question! Because so much adding and multiplying is involved, with such huge numbers, that we had to wait for high-speed computers. If you’d given abacuses to Adam and Eve and all their descendants right up to now, they couldn’t have found some of the pictures Ada can show you by pressing a few keys. Go ahead, dear…”

The holoprojector was cunningly concealed; Bradley could not even guess where it was hiding. Very easy to make this old castle a haunted one, he thought, and scare away any intruders. It would beat a burglar alarm.

The two crossed lines of an ordinary x-y diagram appeared in the air, with the sequence of integers 0, 1, 2, 3, 4… marching off in all four directions.

Ada gave Bradley that disconcertingly direct look, as if she were once again trying to estimate his I.Q. so that her presentation could be appropriately calibrated.

“Any point on this plane,” she said, “can be identified by two numbers—its x- and y-coordinates. Okay?”

“Okay,” Bradley answered solemnly.

“Well, the M-Set lies in a very small region near the origin—it doesn’t extend beyond plus or minus two in either direction, so we can ignore all the larger numbers.”

The integers skittered off along the four axes, leaving only the numbers one and two marking distances away from the central zero.

“Now suppose we take any point inside this grid, and join it to the center. Measure the length of this radius—let’s call it r .”

This, thought Bradley, is putting no great strain on my mental resources. When do we get to the tricky part?

“Obviously, in this case r can have any value from zero to just under three—about two point eight, to be exact. Okay?”

“Okay.”

“Right. Now Exercise One. Take any point’s r value, and square it. Keep on squaring it. What happens?”

“Don’t let me spoil your fun, Ada.”

“Well, if r is exactly one, it stays at that value—no matter how many times you square it. One times one times one times one is always one.”

“Okay,” said Bradley, just beating Ada to the draw.

“If it’s even a smidgin more than one, however, and you go on squaring it, sooner or later it will shoot off to infinity. Even if it’s 1.0000… 0001, and there are a million zeros to the right of the decimal point. It will just take a bit longer.

“But if the number is less than one—say .99999999… with a million nines—you get just the opposite. It may stay close to one for ages, but as you keep on squaring it, suddenly it will collapse and dwindle away down to zero—okay?”

This time Ada got there first, and Bradley merely nodded. As yet, he could not see the point in this elementary arithmetic, but it was obviously leading somewhere.

“Lady—stop bothering Mr. Bradley! So you see, simply squaring numbers—and going on squaring them, over and over—divides them into two distinct sets…”

A circle had appeared on the two crossed axes, centered on the origin and with radius unity.

“Inside that circle are all the numbers that disappear when you keep on squaring them. Outside are all those that shoot off to infinity. You could say that the circle of radius one is a fence—a boundary—a frontier —dividing the two sets of numbers. I like to call it the S-set.”