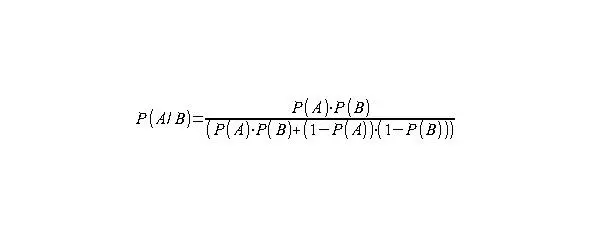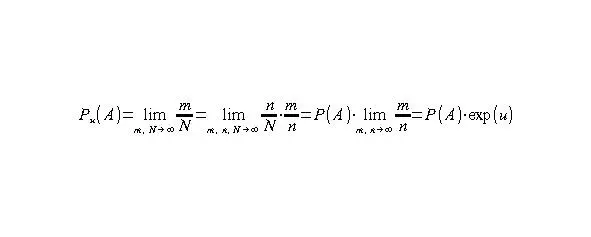Алексей Патрашов: Статьи научные и разные. Сборник

Здесь мы подходим к ещё одному важному понятию, которое нам понадобится для того, чтобы правильно суметь определить знак события, а именно к понятию удачного или неудачного события. Лучше всего знак и величину события получится определять через разность его величины и её математического ожидания. Так мы сможем гораздо лучше определить степень везения или невезения при рассмотрении нескольких однородных событий через их сумму или среднее значение.

Ещё одним очень важным понятием является то, что удача не является не неудачей. То есть играть в лотерею и не выиграть не является неудачей, а скорее закономерностью, поскольку выиграть в лотерею можно чрезвычайно редко. Точно так же не споткнуться на ровном месте не является удачей, а больше является закономерностью потому, что спотыкаются на ровном месте редко.

Также мы должны разобраться в последовательностях событий. Рассмотрим два простых примера. В одном случае пассажир споткнулся, упал, пока поднимался потерял время и опоздал на свой автобус, а в итоге опоздал на самолёт, который в полёте сломался и разбился вместе со всеми пассажирами. В другом случае пассажир так же опоздал на самолёт, который подорвали террористы, которые собирались подорвать именно этот самолёт.

В обоих случаях наблюдается везение после невезения, но в первом случае события не связанные потому, что самолёт мог и не сломаться, а во втором случае связанные потому, что террористы обязательно подорвали бы именно этот самолёт. Так что в первом случае у нас никакого везения нет, а наоборот есть невезение. Падение самолёта было совершенно случайным и окажись опоздавший пассажир на борту, самолёт мог бы и не упасть. А во втором случае катастрофа была бы неизбежна, но пассажир опоздал и ему повезло.

С точки зрения теории вероятностей в первом случае вероятность неудачи была очень мала, а во втором очень велика, поэтому первый случай как предсказанный мы рассматривать не можем, в вот второй как раз почти полностью предсказан. Так что рассматривать два последовательных события как одну цепочку мы можем только в том случае, когда вероятность наступления второго события высока и не зависит от вероятности первого события.

Для лучшего понимания количественных явлений мы напишем несколько схожую с формулой Байеса формулу влияния собственной удачи B участника опыта на вероятность A его исхода.

Для примера несколько рассчитанных случаев покажем в виде таблицы.

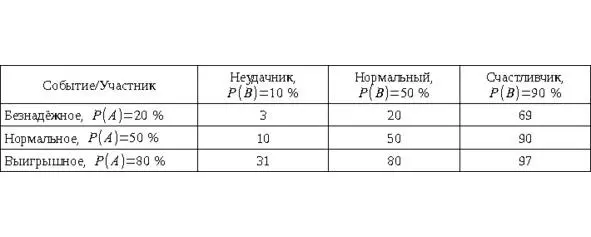
Таблица 1. Успех исхода события P (A/B) в % в зависимости от успешности участника.

Из таблицы видно, что безнадёжное дело неудачник сильно не испортит, а успешное дело счастливчик сильно не улучшит. Само собой надо понимать, что всё сказанное касается в первую очередь крупных событий, то есть приняв за удачное событие выпадение одной стороны монеты, а за неудачное другой, получить перераспределение частоты выпадений в зависимости от удачливости бросающего не получится. Действительно, ведь в падении монеты экспериментатор никак не участвует, а только пытается предсказать результат. Зато вполне возможен вариант выигрыша или проигрыша крупной суммы денег при той же игре в угадывание стороны монеты.

Определение влияния удачи легко получить через расширение классического определение вероятности. Если событие A из N повторов ожидается n раз из расчёта равновозможных исходов, а под влиянием удачи происходит не n, а m раз, то вероятность события A исходя из влияния удачи можно пересчитать как произведение. При этом предполагается, что N, n и m стремятся к бесконечности, поэтому вероятность определяется как предел.

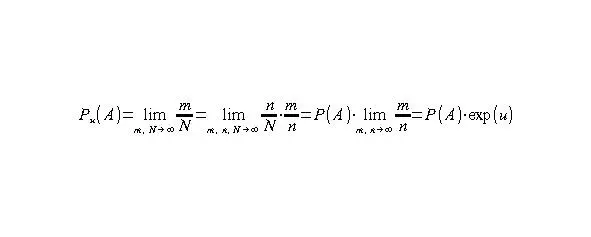
Здесь мы воспользовались условиями, что 0

Если вместо множества событий имеется только набор уже известных вероятностей каждого события, то применить классическое определение вероятности напрямую не получится. Вместо него можно по аналогии применить пересчёт каждой вероятности по очень похожей на формулу Байеса формуле, которая получается при переходе к определению вероятности через её классическое определение, но только через математическое ожидание числа каждого из всех возможных событий из их общего числа N и обратно.