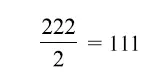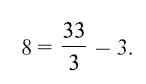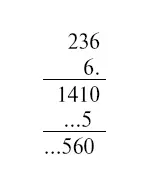за 16-й час причитается 32 768
«17-й ««65 536
«18-й ««131 072
«19-й ««262 144
«20-й ««524 288
Все вместе составляет уже больше миллиона орехов! Но сутки не кончены — остается еще 4 часа.
За 21-й час причитается 1 048 576
«22-й ««2 097 152
«23-й ««4 194 304
«24-й ««8 388 608
А если сложить все 24 часа вместе, то составится 16 777 215 — почти 17 миллионов орехов. Это и будет та тысяча тачек, о которой говорил Степка.
Как получить 20? (60)
Вот как это надо сделать (зачеркнутые цифры заменены нулями):
011
000
009
Действительно: 11 + 9 = 20.
Ив семи цифр (61)
Задача имеет не одно, а три разных решения. Вот они:
123 + 4–5 — 67 = 55;
1 — 2–3 — 4 + 56 + 7 = 55;
12 — 3 + 45 — 6 + 7 = 55.
Пятью единицами (62)
Написать число 100 пятью единицами очень просто:
111 — 11 = 100.
Пятью пятерками (63)
5 × 5 × 5 — (5 × 5).
Это равно 100, потому что 125 — 25 = 100.
Пятью тройками (64)
33 × 3 + 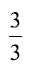 = 100
= 100
Пятью двойками (65)
22 + 2 + 2 + 2 = 28.
Четырьмя двойками (66)
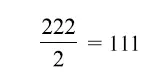
Четырьмя тройками (67)

Мы привели здесь только по одному решению, но можно придумать и еще. Например, число 8 можно составить не только так, как здесь показано, но еще и иначе:
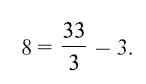
Четырьмя четверками (68)
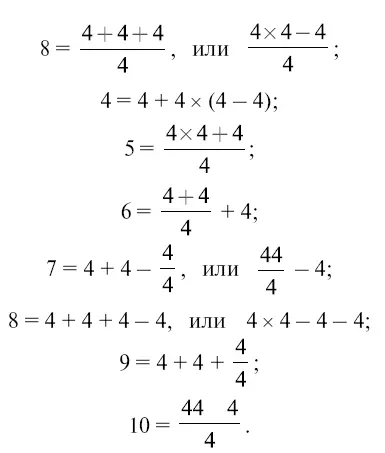
Который год? (69)
Будет только один такой год в XX веке: 1961-й.
В зеркале (70)
Единственные цифры, которые не искажаются в зеркале, — это 1, 0 и 8. Значит, искомый год может содержать в себе только такие цифры. Кроме того, мы знаем, что это один из годов XIX века, т. е. что первые его две цифры 18.
Легко сообразить теперь, какой это год: 1818-й. В зеркале 1818 год превратится в 8181-й: это ровно в 4 1/ 2раза больше, чем 1818:
1818 × 4 1/ 2= 8181.
Других решений задача не имеет.
Какие числа? (71)
Ответ прост: 1 и 7. Других таких чисел нет.
Сложить и перемножить (72)
Таких чисел сколько угодно:
3 × 1 = 3,
3 + 1 = 4,
10 × 1 = 10,
10 + 1 = 11,
и вообще всякая пара целых чисел, из которых одно — единица.
Это потому, что от прибавления единицы число увеличивается, а от умножения на единицу остается без перемены.
Столько же (73)
Числа эти 2 и 2. Других целых чисел с такими свойствами нет.
Три числа (74)
1, 2 и 3 дают при перемножении и при сложении одно и то же:
1 + 2 + 3 = 6; 1 × 2 × 3 = 6.
Умножение и деление (76)
Таких чисел очень много. Например:
2: 1 = 2;
2 × 1 = 2;
7: 1 = 7;
7 × 1 = 7;
43: 1 = 43;
43 × 1 = 43.
Вдесятеро больше (76)
Вот еще четыре пары таких чисел:
11 и 110; 14 и 35; 15 и 30; 20 и 20.
В самом деле:
11 × 110 = 1210;
15 × 30 = 450;
11 + 110 = 121;
15 + 30 = 45;
14 × 35 = 490;
20 × 20 = 400;
14 + 35 = 49;
20 + 20 = 40.
Других решений задача не имеет. Довольно хлопотливо разыскивать решения вслепую. Знание начатков алгебры значительно облегчает дело и дает возможность не только отыскать все решения, но и удостовериться, что больше пяти решений задача не имеет.
На что он множил? (77)
Рассуждаем так. Цифра 6 получилась от сложения колонки из двух цифр, из которых нижняя может быть либо 0, либо 5. Но если нижняя 0, то верхняя 6. А может ли верхняя цифра быть 6? Пробуем: оказывается, чему бы ни равнялась вторая цифра множителя, никак не получается 6 на предпоследнем месте первого частного произведения. Значит, нижняя цифра предпоследней колонки должна быть 5; тогда над ней стоит 1.
Теперь легко восстановить часть стертых цифр:
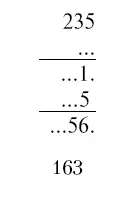
Последняя цифра множителя должна быть больше 4, иначе первое частное произведение не будет состоять из четырех цифр. Это не может быть цифра 5 (не получается 1 на предпоследнем мосте). Пробуем 6 — годится. Имеем:
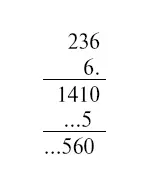
Рассуждая далее подобным же образом, находим, что множитель — 96.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

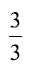 = 100
= 100