События любой игры происходят в определенном пространстве. Это пространство представляет собой «волшебный круг» гейм-плея. Оно определяет собой различные места, в которых существует игра, и то, как эти места соотносятся друг с другом. Будучи игровой механикой, пространство – это еще и математическая конструкция. Нам нужно отбросить все визуальное, всю эстетику и просто посмотреть на абстрактную конструкцию игрового пространства.
Четко определенных правил описания этих абстрактных, упрощенных игровых пространств не существует. Хотя принято считать, что игровые пространства:
1. Могут быть либо дискретными, либо бесконечными;
2. Состоят из некоторого количества измерений;
3. Состоят из разграниченных локаций, которые могут быть соединены или не соединены между собой.
Например, в игре крестики-нолики у нас есть дискретное двухмерное поле. Но что значит «дискретное»? Даже не понимая, что имеется в виду, мы рисуем поле для крестиков-ноликов вот таким.

Это определенно не бесконечное пространство, потому что нас интересуют в первую очередь границы, а не пространство внутри каждой клетки. Куда бы мы ни поставили Х…
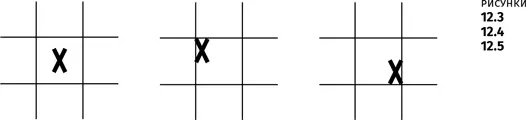
Это не имеет значения – в рамках игры все эти положения эквивалентны. Но если поставить Х сюда…

Это совсем другой случай. Даже несмотря на то что игроки могут ставить свои отметки в любом месте в двухмерном пространстве, существует всего девять дискретных точек, которые имеют значение в игре. В некотором смысле у нас есть девять точечных ячеек, соединенных между собой двухмерной решеткой, как на рисунке ниже.

Каждый круг представляет собой нульмерное место, а каждая линия показывает, какие места соединены между собой. В крестиках-ноликах нет движения от места к месту, но смежность здесь очень важна. Без смежности это были бы просто девять разъединенных точек. Благодаря смежности мы имеем дискретное двухмерное пространство с четко определенными границами: в три клетки длиной и в три клетки шириной. То же самое можно сказать и о пространстве шахматной доски, лишь с тем исключением, что размер этого пространства составляет 8 × 8 клеток.
Яркая эстетика игры может заставить вас подумать, что ее функциональное пространство сложнее, чем оно есть на самом деле. Давайте рассмотрим поле для «Монополии».
С первого взгляда можно подумать, что это дискретное двухмерное пространство, похожее на шахматную доску, с которой убрали большинство центральных клеток. Но ее можно легко представить в виде одномерного пространства – линия из сорока разделенных точек, которые соединены между собой в виде замкнутой петли. Конечно, на игровом поле угловые пространства выглядят несколько иначе, выделяясь среди других ячеек своим размером, но функционально это не имеет значения, поскольку каждая игровая клетка представляет собой нульмерное пространство. Несколько игровых фишек могут стоять на одной клетке, но их взаимное положение внутри этой клетки не имеет функционального значения.
Но не все пространства дискретные. Стол для игры в пул может служить примером бесконечного двухмерного пространства. Он имеет фиксированную длину и ширину, а шар может свободно по нему перемещаться, отскакивая от стенок или падая в лузы, которые тоже находятся в фиксированных местах. Никто не будет спорить с тем, что пространство бесконечное, но является ли оно двухмерным? Поскольку опытный игрок может заставлять шары вылетать за пределы стола и перепрыгивать друг через друга, можно говорить о том, что пространство игры на самом деле трехмерное, и в некоторых случаях подобные рассуждения могут быть полезными. Четких правил для определения этих функциональных пространств не существует. Когда вы создаете новую игру, иногда полезно посмотреть на ее пространство как на двухмерное, но порой представление этого пространства как трехмерного может быть более полезным. То же самое можно сказать о понятиях дискретного и бесконечного пространства. Мы упрощаем игру до набора функциональных пространств для того, чтобы эстетика или реальный мир не мешали нам сосредоточиться на ней. Если вы думаете над тем, как можно изменить футбол, изменив границы игрового поля, вы, скорее всего, думаете об этом в рамках двухмерного бесконечного пространства.
Читать дальше
Конец ознакомительного отрывка
Купить книгу
![Джесси Шелл Геймдизайн [Как сознание определяет наше бытие] [litres] обложка книги](/books/406571/dzhessi-shell-gejmdizajn-kak-soznanie-opredelyaet-na-cover.webp)

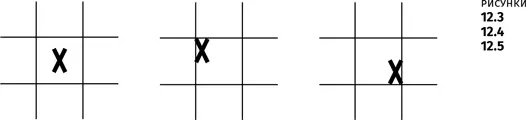





![Сергей Ефременко - Милосердие смерти [Истории о тех, кто держит руку на нашем пульсе] [litres]](/books/393790/sergej-efremenko-miloserdie-smerti-istorii-o-teh-thumb.webp)
![Тимоти С Вайнгард - Кровососы [Как самые маленькие хищники планеты стали серыми кардиналами нашей истории] [litres]](/books/402529/timoti-s-vajngard-krovososy-kak-samye-malenkie-h-thumb.webp)
![Паскаль Буайе - Анатомия человеческих сообществ [Как сознание определяет наше бытие] [litres]](/books/406575/paskal-buaje-anatomiya-chelovecheskih-soobchestv-kak-thumb.webp)
![Джей Эшер - Наше будущее [litres]](/books/424521/dzhej-esher-nashe-buduchee-litres-thumb.webp)
![Медина Мирай - Зазеркалье Нашей Реальности [litres]](/books/430871/medina-miraj-zazerkale-nashej-realnosti-litres-thumb.webp)
![Олег Панков - Как очки убивают наше зрение [litres]](/books/433421/oleg-pankov-kak-ochki-ubivayut-nashe-zrenie-litres-thumb.webp)

