Внутренний СССР - “Грыжу” экономики следует “вырезать”

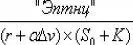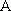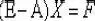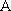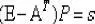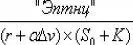
С учетом этого выражение для энергообеспеченности денежной единицы во внутреннем обороте сферы производства следует записать так: .

Что оно означает, можно понять из уравнений межотраслевого баланса. Хотя они не популярны там, где верят в блеф о саморегуляции рынка, и считают их пережитком эпохи Госплана, но тем не менее они позволяют увидеть и объяснить многое, вследствие чего заправилы Запада присудили В.Леонтьеву за работы на их основе нобелевскую премию, которая, кстати, выплачивается из паразитических доходов с “ценных” бумаг. Уравнения межотраслевого баланса представляют собой математический эквивалент схемы продуктообмена рис. 1 и выглядят так:

???? ?? Х = а Х + а Х +… + а X + F ?? Х = а Х + а Х +… + а X + F ?… (1) ? ?? Х = а Х + а Х +… + а X + F

Здесь Х ,…, X — валовый выпуск отраслей с первой по n —ную. Правая часть каждого из уравнений характеризует распределение продукции соответствующей отрасли между ее потребителями:

1) всем набором отраслей в сфере производства — столбцы, содержащие валовые выпуски отраслей Х ,…, X Xj , умноженный на а i j ;

2) продукцией конечного потребления, ради которой и ведется в обществе производство — столбец F ,…, F .

В этой системе второй коэффициент первого уравнения а — численно равен количеству продукта отрасли № 1, необходимого отрасли № 2 для производства единицы учета продукции отрасли № 2. Все остальные коэффициенты а а а имеют тот же смысл и называются коэффициентами прямых затрат . Каждый из них характеризует культуру производства отрасли-потребителя: сколько необходимо продукции отрасли-поставщика по технологии + сколько будет украдено + сколько будет утрачено по бесхозяйственности.

Если каждое уравнение в балансе с натуральным учетом продукции умножить почленно на цену продукта (спектра производства отрасли в целом), производимого соответствующей уравнению отраслью, то система (1)характеризует источники доходов отрасли от продажи ею продукции при рассмотрении соответствующей строки; а столбец, соответствующий номеру отрасли, характеризует ее расходы по оплате продукции, приобретаемой ею у поставщиков в обеспечение ее собственного производства.

После этого ниже системы уравнений можно выписать еще несколько строк функционально обусловленных расходов , производимых отраслью помимо оплаты продукции ее поставщиков в процессе ее собственного производства, о которых неоднократно говорилось ранее:

· Фонд заработной платы.

· Фонд развития и реконструкции производства.

· Финансирование совместных программ.

· Благотворительность.

· Свободные, нераспределенные средства.

· Кредитный и страховой баланс (сальдо).

· Баланс налогов и дотаций (сальдо).

Эти записи помещаются ниже строк баланса продуктообмена в столбцах соответствующих отраслей. Так межотраслевой баланс переводится в стоимостную форму учета продукции.

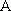
В совокупности коэффициенты прямых затрат образуют квадратную матрицу . И уравнения межотраслевого баланса продуктообмена могут быть записаны в матрично-векторной форме:

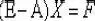
(2),

где: — единичная диагональная матрица, все элементы которой — нули, кроме e = e =… = e = 1 , X и F — векторы-столбцы, спектры производства, вбирающие в себя Х ,…, X и F ,…, F , соответственно. Уравнение ( 2) представляет собой более компактную форму записи ( 1). Она получена переходом к матрично-векторной записи ( 1) после того, как из правой части все члены кроме F во всех уравнениях перенесены в левую часть [81].

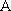
Уравнение ( 2) позволяет ответить на вопрос: каким должен быть спектр валовых мощностей X всех отраслей при культуре производства, описываемой матрицей , чтобы получить спектр конечной продукции F . Если уравнение ( 2) представлено в стоимостной форме учета, то оно дает связь «ЗАТРАТЫ (в их распределении по отраслям) — ВЫПУСК продукции отраслями)», что явилось одним из названий балансового метода.

Возможны балансовые уравнения иного рода:

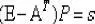
(3),