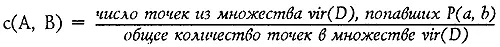Анатолий Фоменко - Истину можно вычислить.

[a i— |a i— b i| — h(a i), а i+ |а i— b i| + h(a i)].

Ясно, что параллелепипед P'(а, b) целиком лежит внутри большого параллелепипеда P(а, b), см. 20. Диагональю этого большого параллелепипеда является вектор а — b + h(а), где вектор h(а) выглядит так:

h(а) = (h(а 1), …, h(a k)).

Его можно назвать ВЕКТОРОМ ОШИБОК ЛЕТОПИСЦЕВ.

Итак, мы смоделировали все три основные ошибки, делавшиеся летописцами при подсчете ими длительностей правлений царей. В качестве окончательного коэффициента с(а, b), измеряющего близость или удаленность друг от друга двух династий а и b, мы возьмем следующее число:

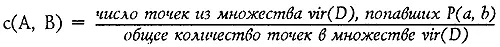
Ясно, что число с(а, b) является интегралом функции плотности z(x) по параллелепипеду P(а, b). На рис. 22 число с(а, b) условно изображается объемом призмы, имеющей в качестве основания параллелепипед P(а, b) и ограниченной сверху графиком функции z. Число с(а, b) можно, при желании, интерпретировать как вероятность того, что случайный «династический вектор», распределенный в пространстве R kс функцией плотности z, оказался на расстоянии от точки а, не превышающем расстояния между точками а и b, с учетом ошибки h(а). Другими словами, случайный «династический» вектор, распределенный с функцией плотности, попал в окрестность P(а, b) точки а, имеющую «радиус» а — b + h(а).

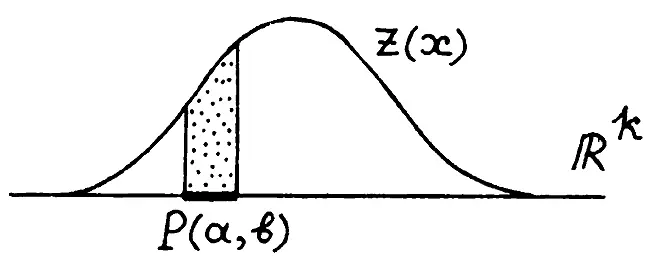
Рис. 22. Представление коэффициента с(а, b) в биде объема «примы», то есть интеграла от функции z(x) по параллелепипеду Р(а, b).

Из предыдущего видно, что роль династий а и b при подсчете коэффициента с(а, b) неодинакова. Династия а была помещена в центр параллелепипеда P(а, b), а династия b определяла его диагональ. Конечно, можно было «уравнять в правах» династии а и b, поступив по аналогии с предыдущим коэффициентом p(X, Y). То есть можно поменять клестами династии а и b, вычислить коэффициент с(b, а), а затем взять среднее арифметическое чисел с(а, b) и с(b, а). Мы этого не делали по двум причинам. Во-первых, показали конкретные эксперименты, замена коэффициента с(а, b) на его «симметризацию» фактически не меняет получающихся результатов. Во-вторых, в некоторых случаях династии a и b действительно могут быть неравноправными в том смысле, что одна из них может быть оригиналом, а вторая — всего лишь ее дубликатом, фантомным отражением. В этом случае естественно помещать в центр параллелепипеда династию а, претендующую на роль оригинала, а «фантомное отражение» b рассматривать как «возмущение» династии а. Возникающие различия между коэффициентами с(а, b) и с(b, а) хотя и невелики, но могут послужить полезным материалом для дальнейших, более тонких исследований, которых мы пока не проводили.

Сформулированный выше принцип малых искажений проверялся на основе коэффициента с(а, b).

1) Для проверки были использованы хронологические таблицы Ж. Блера [76], содержащие практически все основные хронологические данные, в скалигеровской версии, из истории Европы, Средиземноморья, Ближнего Востока, Египта, Азии от якобы 4000 года до н. э. до 1800 года н. э. Эти данные были затем дополнены списками правителей и их правлений, взятых нами из других источников и монографий, как средневековых, так и современных. Упомянем здесь, например, следующие книги: Ш. Бемон, Г. Моно [64], Э. Бикерман [72], Г. Бругш [99], А.А. Васильев [120], Ф. Грегоровиус [195], [196], Д. Эссад [240], Ш. Диль [247], Кольрауш [415], С.Г. Лозинский [492], Б. Низе [579], В.С. Сергеев [766], [767], Chronologie egipticnnc [1069], F.K. Ginzel [1155], LIdeler [1205], L’art de verifier les dates faites historiques [1236], T. Mommsen [1275], Isaac Newton [1298], D. Petavius [1337], I. Scaliger [1387].

2) Как мы уже отмечали, под династией мы понимаем последовательность фактических правителей страны, безотносительно к их титулатуре и родственным связям. В дальнейшем мы иногда будем, для краткости, условно называть их царями.

3) Из-за наличия соправителей иногда возникают трудности при расположении царей в ряд. Мы приняли простейший принцип упорядочения — по серединам правлений.

4) Последовательность чисел, выражающих длительности правлений всех правителей на протяжении всей истории данного государства (то есть длина последовательности априори не ограничивается), будем называть ДИНАСТИЧЕСКИМ ПОТОКОМ. Подпоследовательности, получающиеся отбрасыванием тех или иных СОПРАВИТЕЛЕЙ, назовем ДИНАСТИЧЕСКИМИ СТРУЯМИ. От каждой такой струи требуется, чтобы она была МОНОТОННОЙ, то есть, чтобы середины периодов правлений монотонно возрастали. Требуется также, чтобы династическая струя была ПОЛНОЙ, то есть, чтобы она без пропусков и разрывов покрывала весь исторический период, охваченный данным потоком. Перекрытия периодов правлений при этом допускаются.