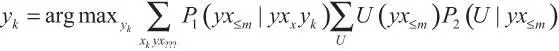Ник Бостром - Искусственный интеллект. Этапы. Угрозы. Стратегии

Или попытаться создать такую систему мотивации, чтобы ИИ был индифферентен к замене целей; см.: [Armstrong 2010].

Мы опираемся на объяснения, данные Дэниелом Дьюи [Dewey 2011]. Использованы также идеи из работ: [Hutter 2005; Legg 2008; Yudkowsky 2001; Hay 2005].

Чтобы избежать ненужного усложнения, мы остановимся на агентах с детерминированным поведением, которые не дисконтируют будущее вознаграждение.

С математической точки зрения поведение агента можно формализовать при помощи агентской функции , ставящей в соответствие каждой возможной истории взаимодействий свое действие. Явно задать агентскую функцию в табличном виде невозможно за исключением случаев самых простых агентов. Вместо этого агенту дается возможность вычислить, какое действие лучше выполнять. Поскольку способов вычисления одной и той же агентской функции может быть много, это ведет к индивидуализации агента в виде агентской программы . Агентская программа — это такая программа или алгоритм, которая вычисляет действие, соответствующее каждой истории взаимодействий. Хотя часто удобнее и полезнее — с математической точки зрения — считать, что агент взаимодействует с другими в некоторой формально определенной среде, важно помнить, что это является идеализацией. На реальных агентов действуют реальные физические стимулы. Это означает не только, что агент взаимодействует со средой посредством датчиков и исполнительных механизмов, но также, что «мозг» или контроллер агента сам является частью физической реальности . Поэтому на его поведение, в принципе, могут воздействовать физические помехи извне (а не только объекты восприятия, или перцепты, полученные с датчиков). То есть с какого-то момента становится необходимым считать агента реализацией агента . Реализация агента — это физическая структура, которая в отсутствие влияния среды выполняет агентскую функцию. (Определения даны в соответствии с работой Дэниела Дьюи [Dewey 2011].)

Дьюи предлагает следующее определение оптимальности для агента, обучающегося ценностям:

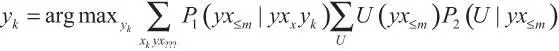
Здесь P 1и P 2— две вероятностные функции. Вторая сумма располагает в определенном порядке некоторый подходящий класс функций полезности по всем возможным историям взаимодействия. В версии, представленной в тексте, мы явно выделили некоторые зависимости, а также упростили обозначение возможных миров.

Нужно заметить, что набор функций полезности U должен быть таким, чтобы полезность можно было сравнивать и усреднять. В принципе, это непросто, кроме того, не всегда очевидно, как представлять различные этические теории в терминах количественно выраженной функции полезности. См., например: [MacAskill 2010].

В более общем случае нужно обеспечить ИИ адекватным представлением условного распределения вероятностей P ( v ( U ) | w ), поскольку v не всегда может напрямую дать ответ, истинно ли утверждение v ( U ) в мире w для любой пары «возможный мир — функция полезности» ( w , U ).

Рассмотрим вначале Y — класс действий, возможных для агента. Одна из сложностей связана с тем, что именно следует считать действием: только базовую моторную команду (вроде «отправить электрический импульс по каналу вывода #00101100») или команду более высокого уровня (вроде «удерживать фокус камеры на лице»)? Поскольку мы скорее пытаемся дать определение оптимальности, а не разработать план практического применения метода, можно ограничить область только базовыми моторными командами (а поскольку набор таких команд может со временем меняться, нам следует проиндексировать Y по времени). Однако чтобы двигаться в сторону практической реализации, очевидно, будет необходимо создать некий процесс иерархического планирования, в рамках которого придется решить, как применять формулу к классу действий более высокого уровня. Еще одна сложность связана с тем, как анализировать внутренние действия системы (вроде записи данных в рабочую память). Поскольку внутренние действия могут иметь важные последствия, в идеале хотелось бы, чтобы в Y были включены и базовые внутренние действия, и моторные команды. Но есть определенные пределы, как далеко можно зайти в этом направлении — вычисление ожидаемой полезности любого действия из Y требует выполнения многочисленных вычислительных действий, и если каждое из них также считается действием из Y , которое должно быть оценено в соответствии с моделью ИИ-ОЦ, мы имеем дело с бесконечной регрессией, которая вообще не позволит тронуться с места. Чтобы исключить эту ситуацию, нужно сузить количество явных попыток оценить ожидаемую функцию полезности ограниченным количеством наиболее важных возможностей для совершения действий. После этого систему нужно наделить некоторым эвристическим процессом, который определит список наиболее важных возможностей совершения действий для дальнейшего рассмотрения. (В конечном счете система могла бы сама принимать решения относительно некоторых возможных действий и вносить изменения в этот эвристический процесс, чтобы постепенно приближаться к идеалу, описанному в модели ИИ-ОЦ.)