Василий Чистяков - Рассказы о математиках

Академик Ю. В. Линник является достойным продолжателем знаменитой петербургской математической школы, основателем которой был П. Л. Чебышев. Для этой школы характерны поиски решения труднейших задач теории чисел по возможности простейшими методами.

Одним из интересных и довольно трудных вопросов теории чисел является вопрос о представлении целых положительных чисел квадратичными формами:

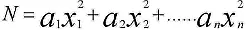
где N и a i — заданные целые числа; х i принимает целочисленные значения.

Эти формы отличаются по числу переменных и называются: при двух переменных — бинарной, при трех — тернарной, при четырех — кватернарной. Самый интересный случай, используемый в кристаллографии, дает тернарная квадратичная форма, решение которой долгое время не поддавалось усилиям многих крупнейших математиков мира. Проблема представимости целого числа тернарной квадратичной формой и была решена Линником в 1939 году.

Французский математик Лагранж более ста лет назад доказал, что всякое натуральное число может быть представлено в виде суммы не более четырех квадратов натуральных чисел. Возник вопрос: сколько надо k-тых степеней натуральных чисел, чтобы представить их суммой всякое натуральное число. Эту проблему поставил английский математик Варинг.

Проблема Варинга была решена в 1908–1909 годах немецким математиком Д. Гильбертом, то его решение было очень громоздким и малопонятным. Академик И. М. Виноградов в 1934 году дал новое решение проблемы Варинга, но оно по-прежнему оставалось очень сложным и опиралось на аппарат высшей математики. В 1943 году Ю. В. Линнику наконец удалось решить эту проблему элементарными средствами, вполне доступными для понимания учащихся.

Ю. В. Линник получил важные результаты также по труднейшим вопросам распределения простых чисел в натуральном ряду и в арифметической прогрессии с разностью d, взаимно простой с первым членом. Им, в частности, доказана теорема о величине наименьшего простого числа в этой прогрессии.

Кроме теории чисел, профессор Линник успешно занимается вопросами теории вероятностей. В частности, пользуясь теорией вероятностей, в 1959 году Ю. В. Линник решил проблему, поставленную в 1923 году английскими математиками Харди и Литлвудом. Решенную проблему Линник сформулировал в виде следующей теоремы: каждое достаточно большое натуральное число N может быть представлено в виде суммы простого числа и двух квадратов натуральных чисел, т. е. в виде N = р + k 2+ l 2.

Увлекаться математикой Игорь Шафаревич стал не сразу. В школе он занимался с «перебоями». Были случаи, когда по математике получал неудовлетворительные оценки. И не потому, что математика давалась ему трудно. Вовсе нет. Просто до математики у него не доходили руки. Причина была ясна: Игорь Шафаревич увлекался тоща историей. Книги по истории приковали его внимание. Читал их молодой Шафаревич и не мог начитаться. Кончал одну книгу, брался за другую и так изо дня в день.

Но в душе Игорь Шафаревич не был доволен собой: неудобно перед учителями и своими товарищами отставать по математике. Надо временно оторваться от истории и наверстать упущенное. И Игорь занялся математикой. Пришлось заниматься самостоятельно. И вот тогда-то произошел перелом. Незаметно для самого себя Игорь увлекся математикой. Он с удовольствием штурмовал математические учебники и с интересом решал задачи, в особенности те из них, которые давались не сразу.

Ему по душе пришлась логическая сторона математики. В особенности своей логической стороной поражала геометрия. Цепь логических умозаключений пронизывает эту науку от самого основания до головокружительных высот. Сколько можно вывести новых интересных теорем! Счету нет! И всему этому мы обязаны нашим рассуждениям, нашей логике. Алгебра! Оперируя символами, в этой науке путем логических рассуждений можно творить чудеса. Ну, окажите, разве все это не интересно?

И Игорь решил изучить школьный курс математики досрочно. Верный своему слову, обладая исключительной памятью, упорством и настойчивостью, он завершил изучение школьного курса математики, когда ему было всего 14 лет.