Валентин Бажанов - Николай Александрович Васильев (1880—1940)

Основным делением суждений, следовательно, надо считать деление на суждения о фактах и на суждения о понятиях, у которых «совершенно различная логика» (сказанное относится и к единичным суждениям).

Логики привыкли устанавливать отношение между суждениями различного качества и количества (А, E, I, О) с помощью «квадрата противоположностей», в котором отношение между А и Е называется отношением противности; отношение между I и О — отношением подпротивности; отношение между А и О, Е и I — отношением противоречия; отношение между А и I, Е и О — отношением подчинения (рис. 2).

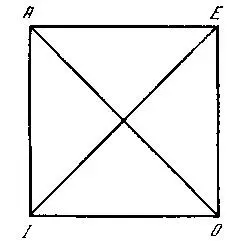
Рис. 2. «Логический квадрат»

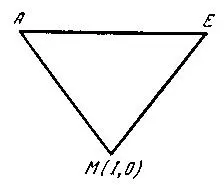
Рис. 3. «Логический треугольник»

Согласно учению традиционной логики, противные суждения могут быть оба ложными, но не могут быть оба истиннымрг; противоречащие суждения не могут быть оба истинными, но и не могут быть оба ложными; подпротивные суждения могут быть оба истинными, но не могут быть оба ложными; из истинности подчиняющего суждения (А, Е) следует истинность подчиненного (но не обратно), а из ложности подчиненного (I, О) следует ложность подчиняющего.

Н. А. Васильев выражает удивление, что эти правила почему-то ни у кого не вызывают сомнения, хотя для суждений о понятиях верно только первое, остальные неверны. Например, правило относительно противоречащих суждений. Конечно, ясно, что они не могут быть оба истинными, но они также могут быть оба и ложными. Два суждения: «Все треугольники имеют сумму углов 360°», «Некоторые треугольники не имеют сумму углов в 360°» — находятся в отношении противоречия, но они оба ложны. Последнее суждение, как было выяснено чуть выше, заключает в себе также смысл, что существуют некоторые треугольники, которые имеют сумму углов в 360°, а это «явная нелепость». Кроме того, между I и О нет никакой противоположности: они слиты в одном суждении М. В этом случае остальные пары противоположностей (А, Е; А, М; Е, М) подчинены одному-единственному правилу: оба суждения не могут быть истинными, но могут быть оба ложными. Стало быть, отношение между суждениями о понятии выражается с помощью «треугольника противоположностей» (рис. 3).

Что касается «квадрата противоположностей», то он отражает отношение между общими и неопределенными и (или) неопределенно-числовыми суждениями. Квадрат верен в том случае, когда слово «некоторые» употребляется в смысле «некоторые, а может быть, и все S суть Р».

Для суждений о фактах остается справедливым закон исключенного третьего; для суждений о понятиях же необходим закон исключенного четвертого, поскольку ложность двух суждений в треугольнике влечет истинность третьего. Вообще закон исключенного третьего чаще других логических законов подвергался обсуждению и вызывал наиболее резкие разногласия. «Между тем - закон исключенного третьего должен быть совершенно удален из скрижали законов мысли, — провозглашает Н. А. Васильев и продолжает: — Я, конечно, рискую, утверждая это, подпасть под обвинение в логической ереси или даже в чем более худшем, что, конечно, страшно для всякого, а тем более для начинающего, но моя логическая совесть не позволяет мне мириться с этим „законом мысли"» [11, с. 41].

Любой предикат может трояко относиться к любому субъекту (понятию): либо он для него необходим (тогда получается утвердительное суждение), либо невозможен (отрицательное суждение), либо же возможен (акцидентальное суждение). Констатация того, что одно из этих суждений должно быть истинно, а четвертого образовать нельзя, и есть закон исключенного четвертого, естественным образом вытекающий из «треугольника противоположностей». Закон исключенного третьего применим только к фактам, реальности.

Брошюра (статья) Н. А. Васильева «О частных суждениях, о треугольнике противоположностей, о законе исключенного четвертого», несмотря на свой сравнительно небольшой объем, дает абрис новой логики. В ней в достаточно компактном виде содержатся многие ключевые положения неаристотелевой логики Н. А. Васильева — деление суждений на суждения о понятиях и о фактах, причем каждый вид деления подчиняется особой логике: в первом случае имеет место закон исключенного четвертого, а во втором — закон исключенного третьего; новое понимание частных суждений, которое также предполагает их отличную от традиционной классификацию.