Анатолий Фоменко - Как было на самом деле. Каждая история желает быть рассказанной

Рис. 3.138. А. В. Болсинов и А. Т. Фоменко. Германия, Бонн, 19 августа 1998 года.

Рис. 3.139. Трехосный эллипсоид.

А что такое задача Эйлера? Рассмотрим динамику тяжелого твердого тела, закрепленного в его центре масс. Тогда движение тела описывается так называемыми дифференциальными уравнениями Эйлера. Важными частными случаями этой задачи являются, например, описание поведения корабля в океане, свободного полета самолета, то есть с выключенными двигателями и т. п., рис. 3.140, рис. 3.141.

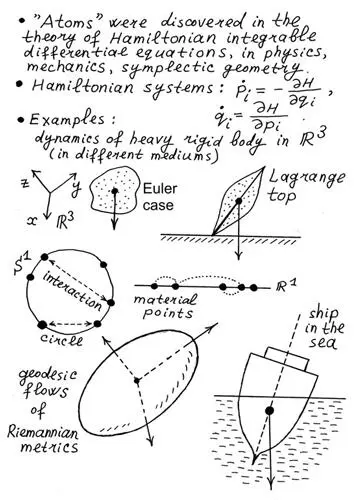
Рис. 3.140. Фрагмент тезисов моего доклада на международной топологической конференции в Греции 2010 года, где говорится о доказанной нами траекторной эквивалентности задач Эйлера и Якоби.

Рис. 3.141.Свободный полет самолета хорошо описывается уравнениями Эйлера. Случай Эйлера – это движение твердого тела, закрепленного в центре масс.

С точки зрения симплектической геометрии эта система уравнений Эйлера является динамической системой на том же четырехмерном фазовом пространстве, являющемся кокасательным пучком двумерной сферы. Таким образом, на одном и том же 4-мерном многообразии есть две замечательные системы уравнений, каждая из которых описывает свою «задачу». Обе эти задачи на первый взгляд кажутся совершенно различными и на протяжении многих лет, начиная с XIX века, изучались самостоятельно, без всякой связи одна с другой. И вот, совершенно неожиданно, применяя созданную мной теорию топологической классификации интегрируемых систем, мы обнаружили, что эти две динамические системы непрерывно траекторно эквивалентны.

Иными словами, имеется гомеоморфизм указанного четырехмерного пространства на себя, переводящий интегральные траектории одной системы в интегральные траектории другой системы. При этом параметр-время движения вдоль траекторий сохраняться не обязан.

Более того, мы показали, опираясь на важные результаты А. В. Болсинова, что с гладкой точки зрения эти системы траекторно не эквивалентны! То есть существует гомеоморфизм, переводящий интегральные траектории задачи Якоби в интегральные траектории случая Эйлера, но нет диффеоморфизма. Тем самым обнаружилось чрезвычайно тонкое различие между топологическими и гладкими свойствами этой известной системы.

В целом, получился яркий и глубокий результат. Между прочим, В. И. Арнольд был задет и раздражен, когда я сообщил ему эту нашу теорему и предложил ему наш подробный доклад на эту тему на его семинаре на мехмате. Однако Арнольд с ходу отказался нас выслушать, заявив, что хотя результат действительно яркий, но он считает, что «этот факт должен быть доказан по-другому, без использования теории Фоменко классификации интегрируемых систем». Я удивился такой форме отказа. Кстати, насколько мне известно, другого доказательства этого нашего результата до сих пор нет.

Тот факт, что в двойственном отношении Арнольда ко мне большую роль играла именно ревность, отмечали некоторые математики, близко знавшие Арнольда. В частности, как мне потом объяснили мои старшие коллеги по Академии (в частности, С. М. Никольский), именно из-за этой ревности Арнольд неожиданно выступил против меня на собрании Отделения во время выборов в академики, хотя буквально за день до этого, во время обсуждения кандидатур, сам же признавал, в присутствии свидетелей, что работы Фоменко – очень хорошие, и четко говорил, что собирается голосовать за меня. Но за одну ночь переменил мнение на противоположное. Наверное, поддался эмоциям.

Поездка в США, в Нью-Йорк, в Dowling College, 3–10 марта. Прочел несколько лекций по наглядной и компьютерной геометрии. В Anthony Giordano Gallery была организована выставка моих графических работ (около полуторы сотни листов). Был большой успех, много посетителей, особенно молодежи, студентов. Вот фрагмент рекламного плаката: «Dr. Anatoly T. Fomenko. A noted Soviet mathematician with a talent for expressing abstract mathematical concepts through artwork. Creativity in Art and Mathematics».

Поездка вместе с Таней в Германию, г. Бонн, в известный математический центр, институт Макса Планка, с 25 июня по 6 августа. Доклады по математике, совместная научная работа с учеными из института. Приглашал директор института профессор Ф. Хирцебрух, знаменитый математик, рис. 3.142, рис. 3.143. Вообще он и раньше много раз предлагал мне приехать в Германию на конференции и для чтения лекций, начиная с того времени, когда я был еще аспирантом. Но в те годы выезд за рубеж для меня был затруднен, и ранее не удавалось реализовать его многочисленные приглашения.