А разве может быть жизнь полнокровной без путешествий? И в конце лета 1929 г. Амбарцумян, Бронштейн, Козырев и Кибель отправились в путешествие по Армении к селу Басарчегар (ныне — Варденис) — родному селению В. А. Амбарцумяна. Перед отъездом из Ленинграда они сфотографировались. Хотя путешествие было недолгим (чуть больше недели), в нем было все необходимое: и плаванье на корабле (по Севану), во время которого поднялась буря и качка достигала почти океанских масштабов, и верховая езда, и ночь под открытым небом, которую пришлось коротать, рассказывая по очереди страшные истории, и 40-километровый пеший переход. Во время этого путешествия М. П. Бронштейну, не отличавшемуся спортивной подготовкой, не раз приходилось недостаток физических сил восполнять духовными. Но зато была достигнута главная цель — забраться подальше от Ленинграда, от науки и отдохнуть от напряженной работы. Ко многому они могли относиться несерьезно, но только не к науке. А серьезное отношение предполагает труд, труд постоянный, в полную силу.
2.4. Первые работы по астро-, гео- и популярной физике
1929 год был для Бронштейна напряженным и продуктивным. Этим годом помечены две его работы по астрофизике и одна по геофизике; в этом же году вышла его первая популярная книга и несколько статей (напомним, что он тогда был еще студентом!).
Первые астрофизические работы Бронштейна посвящены атмосферам звезд 5. В этой же области работали тогда Амбарцумян и Козырев. В то время физика энергично и всерьез рассматривала новый для себя объект — звезду как целостную физическую систему. Прежде чем решать главный астрофизический вопрос о внутреннем строении и об источнике энергии звезды, надо было начать с ее начала — с поверхности звезды, с ее атмосферы, связывающей звезду с внешним миром, и в частности с наблюдателем. Без ясного количественного понимания «поверхностных» астрофизических явлений нельзя было рассчитывать на успешное продвижение в глубь звезды. С другой стороны, и сама физика тогда была уже достаточно развита для рассмотрения процессов в атмосфере звезды, но совершенно недостаточно — для раскрытия ее внутреннего устройства.
Теория звездной атмосферы стала тогда уже вполне респектабельной областью, в которой нельзя было рассчитывать на успех с налету. Надо было внимательно изучить сделанное предшественниками. Здесь уже успели появиться свои классики: К. Шварцшильд, Дж. Джинс, А. Эддингтон, Э. Милн.
Задача о лучистом равновесии звездной атмосферы, которой занялся Бронштейн, восходит к Шварцшильду (тому самому, кстати, который получил первое точное решение уравнений ОТО). В астрофизике звезду (и в частности Солнце) принято характеризовать эффективной температурой Т э ф — температурой черного тела, имеющего те же размеры и такое же полное излучение, что и данная звезда. Величина Т эф просто рассчитывается исходя из земных наблюдений. Задача, которая привлекла внимание Бронштейна, состояла в отыскании зависимости температуры вещества звезды от (оптической) глубины т, разумеется, в рамках определенной физической модели звезды. К тому времени было уже известно, что эта зависимость имеет вид
Т (т) = Т эф [ 3/4(т + д(т))] 1/4
5Авторы этой книги глубоко благодарны В. В. Иванову за подробный комментарий к первым астрофизическим работам Бронштейна.
где величина д(т) мало меняется и дается решением определенного интегрального уравнения (уравнения Милна). Ясно, что численное значение q(0) дает возможность по измеряемой на Земле величине ТЭф узнать истинную температуру поверхности Солнца T o . На определение величины q(0) были затрачены многие усилия корифеев астрофизики, но удавалось получить только различные приближения (по два — Джинс и Эддингтон и три — Милн). И вот Бронштейн в 1929 г. получил точное значение 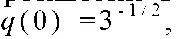 а следовательно, и точное соотношение
а следовательно, и точное соотношение
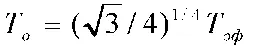
Этот результат впоследствии стал называться соотношением Хопфа— Бронштейна [297, с. 85, 96], хотя порядок фамилий мог быть и обратным, потому что Хопф [10] Выдающийся немецкий математик Э. Хопф (род. 1902) в то время работал в Берлинском университете. Из его занятий математическими вопросами переноса излучения выросли уравнение и метод Винера—Хопфа.
получил его несколько позже .
Читать дальше

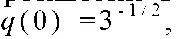 а следовательно, и точное соотношение
а следовательно, и точное соотношение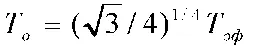





![Матвей Бронштейн - Солнечное вещество и другие повести, а также Жизнь и судьба Матвея Бронштейна и Лидии Чуковской [сборник]](/books/431099/matvej-bronshtejn-solnechnoe-vechestvo-i-drugie-poves-thumb.webp)




