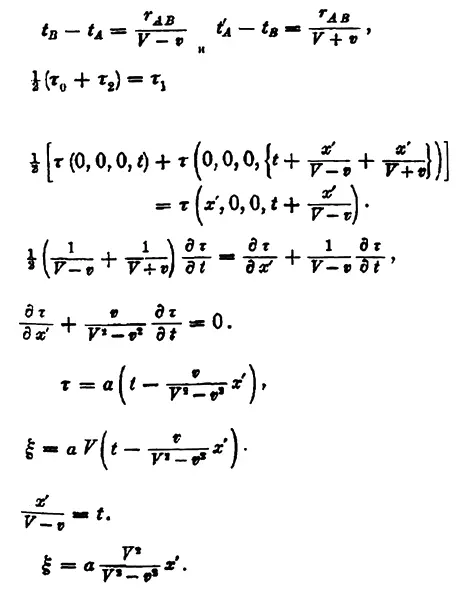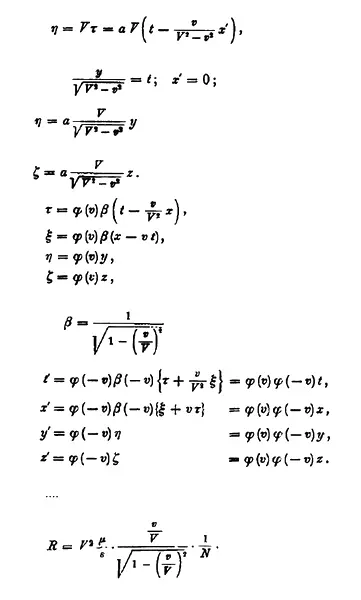Максим Чертанов - Эйнштейн

Ладно, давайте признаем правоту Планка, и дело с концом; но не дает треклятый Максвелл со своими уравнениями! У него свет — гладкий и непрерывный! Признать, что правы и Планк, и Максвелл? Свет — и волна, и частица? Не могли тогдашние физики на такое пойти: уравнения-то не сходятся. А обывателю как раз легко это вообразить: волна воды состоит же из молекул воды, что тут странного? На самом деле все сложнее: волна света не «состоит» из частиц, она и есть частица, а частица — волна. Но если не можете этого представить — и не надо. Останемся с нашим обывательским пониманием и поверим Эйнштейну. А физики не поверили. Сам Планк и то усомнился.

Эйнштейн отправил статью о квантах света в «Анналы» 17 марта 1905 года (напечатают ее в июле) и продолжал думать о том, как помирить Максвелла со всей физикой, то бишь об эфире, которого нет, и о движении и времени, рассуждая примерно так же, как и Пуанкаре; 18 мая писал Габихту, что до конца года собирается опубликовать еще четыре статьи — «несуразный лепет». 30 апреля закончил вторую статью — «Новое определение размеров молекул»; как вспоминала Майя (она получила диплом учительницы и собиралась продолжать образование за границей), он понял, что жить без диссертации не комильфо, хотел взять темой движение и время, но в Цюрихском университете тему отвергли как слишком умозрительную, и 20 июля он предложил Кляйнеру эти самые размеры молекул. (Диссертацию с посвящением Марселю Гроссману опубликовали «Анналы» в 1906 году.) По легенде, идея возникла, когда Эйнштейн пил чай и понял, что если знать объем чашки и скорость растворения сахара, можно рассчитать количество и размер молекул сахара в чашке; осталось только уравнения написать.

11 мая он отправил в «Анналы» третью работу — «О движении взвешенных в покоящейся жидкости частиц, требуемом молекулярно-кинетической теорией теплоты». Как и в случае с фотоэффектом, объяснил явление, которое все давно знали, — броуновское движение: ботаник Роберт Броун заметил хаотическое метание частичек пыльцы в стоячей воде. По Эйнштейну, пыльца металась, сталкиваясь с молекулами жидкости. «Анналы» напечатали статью 18 июля, и вскоре обсудить ее пришел любознательный швейцарец, ставший очередным другом навек — судебный медик Генрих Цангер, человек сильный, уверенный, решительный, отчасти — несмотря на небольшую разницу в возрасте — игравший для Альберта роль условного «отца» и однажды спасший ему жизнь, когда тот угорел от печки.

13 мая Эйнштейны переехали на Безеншвенгештрассе, 28. А 30 июня была окончена (опубликована 26 сентября) знаменитая статья «К электродинамике движущихся тел», в которой изложены основы специальной теории относительности (ее называют СТО, а позже будет еще общая теория относительности — ОТО), где Максвелловы лампочки и намагниченные опилки должны были непротиворечиво сойтись с мчащимися поездами и самолетами.

Перед нами вновь встает проблема языка. Описать процесс работы физика-теоретика так, чтобы его понял гуманитарий, невозможно. Одно дело — примитивно растолковать, «про что» теория относительности, перевести ее на детский язык: + вот стоит человечек на железнодорожной насыпи, светит фонариком; но это не даст нам никакого представления о мышлении ученого. Да, Эйнштейн говорил, что толчком послужила мысль о человеке, оседлавшем солнечный луч, но потом-то он еще год думал и пять недель писал статью… Легко описать, как трудился Дарвин: препарировал жуков и дохлых кур, расспрашивал людей, как передается характер козы и почему улыбаются младенцы, и увидеть, как из этого рождается научная мысль, самим ученым облеченная в понятные слова: «Если мы позволим себе увлечься догадками, то животные — наши собратья по боли, болезни, смерти, страданию и чувству голода, наши рабы в выполнении самых тяжелых работ, наши товарищи в забавах — могут вместе с нами происходить от общего предка, все мы можем быть связаны воедино».

У математиков, теоретических физиков все по-другому. Эйнштейн мыслил, как сам сказал, «психическими сущностями», «более или менее четкими изображениями», которые носят «мышечный» характер. Но даже сами математики не могут напрямую обмениваться «мышечными ощущениями» — они переводят их на свой язык, язык знаков, что уже ближе к человеческому, но как понять его, не будучи математиком? Просто посмотрите, не вникайте…

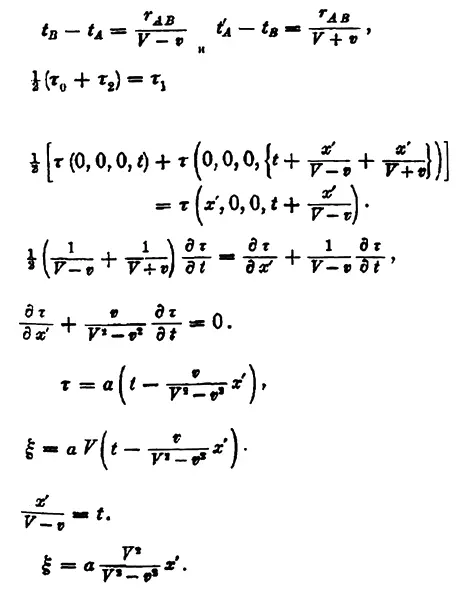
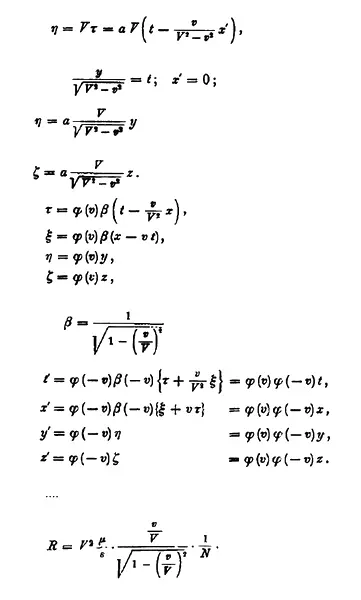
Нет, такой язык нам не годится — нужен язык слов. Такой? «В этот раз он попытался доказать теорему соответственных состояний (лоренц-ковариантность) для неоднородных уравнений Максвелла — Лоренца. При преобразовании уравнений для скоростей он допустил ошибку, в результате чего не получил ковариантности для членов выше первого порядка». Опять не тот язык! Не понимаем! Может, взять язык музыки, раз они с математикой так схожи?