Teacher.elementary.school - Методика преподавания математики в начальной школе

А

В

в) а – «прямая», b – «отрезок»: объемы понятий не пересекаются, т.к. ни про один отрезок нельзя сказать, что он является прямой, и ни одна прямая не может быть названа отрезком. Следовательно, данные понятия не находятся в отношении рода и вида (отрезок – часть прямой, т.е. наблюдается отношение целого и части).

А В

IV . Определение понятий

1. Понятие определения.

Определение понятий – это логическая операция, с помощью которой раскрывается содержание понятия, либо устанавливается значение термина.

2. Виды определений.

По способу выявления содержания понятия различают явныеи неявныеопределения.

К неявным определениям относят остенсивные. Этоопределения, раскрывающие существенные свойства (признаки) предметов путем указания, показа, демонстрации объектов, которые этими терминами обозначают.

Например, при ознакомлении с алгебраическими понятиями пользуются остенсивными определениями так:

4 · 7 < 4 · 9 8 · 7 = 56

23 + 8 > 30 9 · 6 = 6 · 9

93 – 8 < 93 – 6 46 + 7 = 62 – 9

Это неравенства. Это равенства.

Наиболее часто применяются остенсивные определения при изучении геометрических понятий.

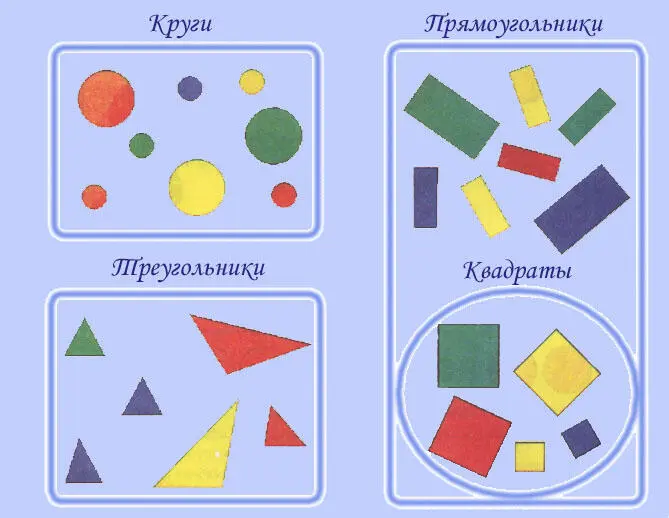
Остенсивные определения характеризуются незавершенностью. Поэтому впоследствии требуется подробное изучение этих понятий.

Также применяют описание или сравнение объектов.

К неявным определениям относят и контекстуальные – через отрывок текста, через контекст, через анализ конкретной ситуации, описывающей смысл понятия.

Через текст устанавливается связь определяемого понятия с другими, уже известными понятиями, раскрывая его содержание.

Например, при изучении понятия уравнения (2 класс):

– 5 = 4

Из какого числа нужно вычесть 5, чтобы получилось 4?

Обозначим неизвестное число латинской буквой х:

х – 5 = 4 – это уравнение.

Решить уравнение – это значит найти неизвестное число. В данном уравнении неизвестное число равно 9, так как 9 – 5 = 4.

Объясни, почему числа 0, 10, 8 не подходят.

3. Определение через род и видовое отличие.

Среди явных определений в математике чаще всего используются определения через род и видовое отличие.

Например: «Прямоугольник – это четырехугольник, у которого все углы прямые».

В этом определении есть две части – определяемое понятие (прямоугольник) и определяющее понятие (четырехугольник, у которого все углы прямые). Если обозначить через а первое понятие, а через b – второе, то данное определение можно представить в таком виде:

а есть (по определению) b или а <=> b

опр.

Читают запись так: « а равносильно b по определению» или « а тогда и только тогда, когда b ».

В определении прямоугольника можно выделить в определяющем понятии:

а) понятие «четырехугольник», которое является родовым по отношению к понятию «прямоугольник»;

б) свойство «иметь все углы прямые», которое позволяет выделить из всевозможных четырехугольников один вид – прямоугольники; поэтому его называют видовым отличием.

Видовое отличие – это свойство (одно или несколько), которые позволяют выделять определяемые объекты из объема родового понятия.

Это можно показать на схеме:

Определяемое понятие <=> Родовое понятие + Видовое отличие

Определяющее понятие

Схему можно заменить формулой: а <=> с + Р

опр. b

Формулируя определения понятий через род и видовое отличие, применяют следующие правила:

1) определение должно быть соразмерным;

2) в определении не должно быть порочного круга;

3) определение должно быть ясным;

4) одно и то же понятие определить через род и видовое отличие, соблюдая правила можно по-разному.

Натуральные числа и 0.

Методика изучения нумерации натуральных чисел и 0 в начальном курсе математики

План:

1. Из истории возникновения и развития понятий натурального числа.

2. Отрезок натурального ряда. Счет элементов конечного множества.

3. Теоретико-множественный смысл натурального числа и нуля.

1. Из истории возникновения и развития понятий натурального числа и нуля

В начальной школе большое внимание уделяется изучению нумерации целых неотрицательных чисел, а также действий над ними. Это является одной из центральных тем курса начальной математики, так как всю жизнь человек пользуется различного рода вычислениями, счетом предметов и т.д. Следовательно, учитель должен хорошо представлять себе, с какой системой счисления он работает, каковы ее особенности и как она появилась.