Инесса Раскина - Логика для всех. От пиратов до мудрецов

Верно ли это «доказательство»?

Задача6*. Конечно или бесконечно множество простых чисел?

Задача 7.Петя сказал: «Если кот шипит, то рядом собака, и наоборот, если собаки рядом нет, то кот не шипит». Не сказал ли он что-то лишнее?

Задача 8.Все знают: когда Петя готов к уроку, он всегда поднимает руку. И вдруг…

1) Двоечник Вася точно знает, что сегодня Петя не готов к уроку. «Значит, он не будет поднимать руку», – думает Вася. Верно ли он рассуждает?

2) Марья Ивановна видит, что Петя не поднимает руку. «Ага, значит, он к уроку не готов. Вот сейчас вызову и двойку поставлю!» – думает коварная Марья Ивановна. Верно ли она рассуждает?

Задача9. В вершинах куба расставлены числа 1, 2, 3, 4, 5, 6, 7, 8. Докажите, что есть ребро, числа на концах которого отличаются не менее чем на 3.

Задача 10.Десять друзей послали друг другу праздничные открытки, так что каждый послал пять открыток. Докажите, что найдутся двое, которые послали открытки друг другу.

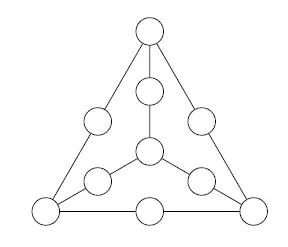
Задача 11.Можно ли в кружочках расставить все цифры от 0до 9 так, чтобы сумма трех чисел на каждом из шести отрезков была бы одной и той же?

Задача 12.Двое играют в игру «Щелк!». У них есть прямоугольная шоколадка, разделенная на дольки. Левая нижняя долька отравлена. Ходят по очереди. За ход можно съесть произвольную дольку и все находящиеся справа и сверху от нее. Съевший отравленную дольку проигрывает. Докажите, что у первого игрока есть выигрышная стратегия на любой прямоугольной шоколадке, в которой больше одной дольки (предъявлять стратегию не обязательно).

Задача 13.Круг разбит на 25 секторов, пронумерованных в произвольном порядке числами от 1 до 25. В одном из секторов сидит кузнечик. Он прыгает по кругу, каждым своим прыжком перемещаясь по часовой стрелке на количество секторов, равное номеру текущего сектора. Докажите, что в некотором секторе кузнечик не побывает никогда.

Задача 14. 1)Несколько мальчиков стали в ряд, при этом разница в росте между двумя соседними не более 10см. Потом их построили по росту. Докажите, что и теперь разница в росте между двумя соседними мальчиками не более 10 см.

2) На уроке танцев 15 мальчиков и 15 девочек построили двумя параллельными колоннами, так что образовалось 15 пар. В каждой паре измерили разницу роста мальчика и девочки (разница берется по абсолютной величине, то есть из большего вычитают меньшее). Максимальная разность оказалась 10 см. В другой раз перед образованием пар каждую колонну предварительно построили по росту. Докажите, что максимальная разность будет не больше 10 см.

Задача 15.Найдите ошибку в рассуждении.

Докажем от противного, что ленивых учеников больше, чем прилежных. Предположим, что прилежных не меньше, чем ленивых. Несомненно, ленивых учеников больше, чем надо. Значит, получается, что прилежных учеников тем более больше, чем надо?! Сэтим мы, учителя, согласиться никак не можем. Получили противоречие, значит, исходное предположение было неверно, и на самом деле ленивых учеников больше, чем прилежных.

Задача 1.1) Известно, что высказывание А ⇒ Б истинно. Что можно сказать об истинности высказываний А ⇒ Б и Б ⇒ А?

2) Известно, что высказывание А ⇒ Б истинно. Можно ли что-то сказать об истинности высказывания А ⇒ Б?

3) Известно, что высказывание А ⇒ Б ложно. Можно ли что-то сказать об истинности высказывания А Б?

Приведите для каждого случая примеры подходящих высказываний.

Задача2. Бабушка печет пирог в те и только те дни, когда ждет гостей.

1) Бабушка печет пирог. Можно ли утверждать, что она сегодня ждет гостей?

2) Бабушка не печет пирог. Можно ли утверждать, что сегодня она не ждет гостей?

Задача 3.Равносильны ли высказывания Аи Б?Если нет, то следует ли хотя бы одно из них из другого?

1) А: «Некоторые принцессы – красавицы»; Б: «Некоторые красавицы – принцессы».

2) А: «Все принцессы – красавицы»; Б: «Все красавицы – принцессы».

3) А: «Число N кратно 11»; Б: «Сумма цифр числа N, стоящих на четных местах, равна сумме цифр, стоящих на нечетных местах».

4) А: «Число N является квадратом натурального числа»; Б: «У числа N нечетное число делителей».

5) А: «У любой девочки из 6 „А“ больше друзей среди одноклассников, чем у любого мальчика из 6 „А“ среди одноклассниц»; Б: «В 6 „А“ мальчиков больше, чем девочек».