Яков Перельман - Головоломки. Фокусы. Задачи. Игры. Развлечения

Если внимательно проследить за выкладками, то легко заметить, что у загадчика должно получиться учетверенное задуманное число да еще 4. Значит, если отнять эти 4 и разделить остальное на 4, то получится задуманное число.

Опять проследим, какие выкладки производились с каждой цифрой. Первая цифра была умножена сначала на 2, потом на 5, потом на 10, т. е. в итоге на 2 × 5 × 10, или на 100. Вторая цифра умножена на 10; третья прибавлена без изменения. Кроме того, ко всему этому прибавлено 5 × 5 × 10, т. е. 250.

Значит, если от полученного числа отнять 250, то останется: первая цифра, умноженная на 100, плюс вторая, умноженная на 10, плюс третья цифра. Короче сказать, останется как раз задуманное число.

Отсюда ясно, как отгадать задуманное число: нужно от результата всех выкладок отнять 250. Получится то, что было задумано.

Чтобы понять, как выполняется в этих случаях отгадывание, проследите, какие действия я заставляю вас проделывать с задуманными цифрами. В первом примере вы сначала умножили цифру на 5; потом то, что получилось, умножили на 2. Значит, вы умножили ее на 2 × 5, т. е. на 10, а всякое число, умноженное на 10, дает результат, оканчивающийся нулем. Зная это, я прошу вас прибавить 7; теперь мне известно, что у вас в уме число из двух цифр: первой я не знаю, а вторую знаю – 7. Неизвестную мне первую цифру я прошу вас зачеркнуть. Что же теперь у вас в уме? Конечно, 7. Я могу уже назвать вам это число, но я хитер; чтобы запутать следы, я прошу вас прибавлять и отнимать от этой семерки разные числа, а сам про себя проделываю то же самое. И наконец, объявляю вам, что у вас получилось 17. Это число у вас обязательно должно получиться, какую бы цифру вы ни задумали.

Второй раз я при отгадывании иду уже другим путем, иначе вы, пожалуй, слишком рано смекнете, в чем секрет. Я заставил вас задуманную цифру сначала утроить, потом полученное снова утроить и к результату прибавить задуманную цифру. Что же, в конце концов, у вас должно составиться? Легко сообразить: ведь это все равно что умножить задуманную цифру на 3 × 3 + 1, т. е. на 10. Опять я знаю, что у вас на конце нуль. Ну а дальше по-старому: прибавляется какая-нибудь цифра, зачеркивается первая неизвестная, а с остающейся, которую я знаю, проделываются для заметания следов разные выкладки.

Третий случай. И здесь то же самое, только на иной лад. Я прошу вас задуманную цифру удвоить, полученное опять удвоить и вновь полученное удвоить снова, а к результату дважды прибавить задуманную цифру. Что же все это дает? Дает вашу цифру, умноженную на 2 × 2 × 2 + 1 + 1, т. е. на 10. Остальное понятно само собою.

Даже если вы задумали 1 или 0, фокус удается безошибочно.

Теперь вы не хуже меня сможете проделывать такие же опыты с теми из ваших товарищей, которые не читали этой книжки. А может быть, придумаете и собственные способы отгадывания. Дело нехитрое.

Дело очень просто: ведь о втором-то пионере забыли! От первого перескочили прямо к третьему, оставив второго без койки.

Вот в чем. Бечевку, связывающую руки товарища А , берут в точке, обозначенной на рисунке буквой й, и продевают через кольцо, охватывая руку В , в том направлении, которое обозначено стрелкой.

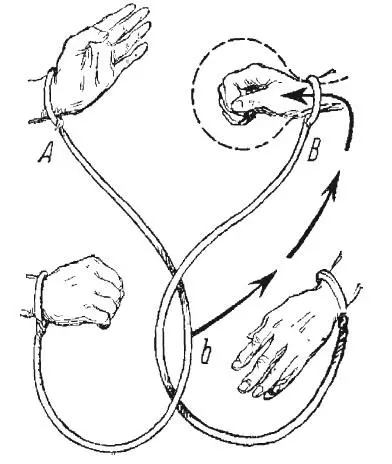
Когда протянута достаточная часть бечевки, в образовавшуюся петлю просовывают руку В и тянут бечевку А. Товарищи разъединяются.

Вот разгадка. Рамку сгибают вдоль пополам так, что одна половина покрывает другую. Сложенные концы продевают через овальное кольцо. Затем между сложенными концами продевают распрямленную фигуру сапог, снова сгибают их, придвигают к перегибу рамки и надвигают на них овальное кольцо, как требуется задачей.

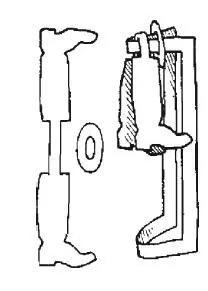
Теперь остается только вновь расправить рамку, и задача решена.

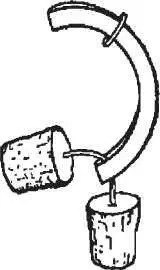
Разгадка такова: надо согнуть бумажное кольцо, снять проволочное колечко, сдвинув его к свободному концу; тогда освободить пробки не составит уже никакого труда.