Яков Перельман - Веселые задачи. Две сотни головоломок

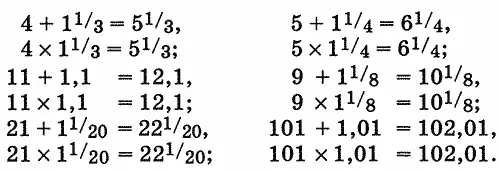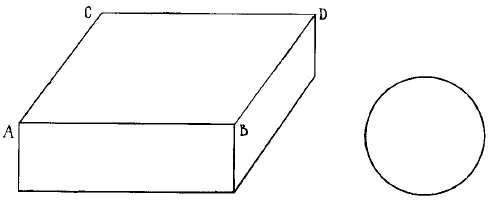
Рис. 201. Поместится ли кружок между АВ и CD?

На рис. 202. вы видите два заштрихованных кружка, которые кажутся одинаковых размеров. Однако вы натренировали свой глазомер предыдущими упражнениями и, конечно, не попадете впросак.

Вам нетрудно будет ответить на вопрос: какой кружок больше?

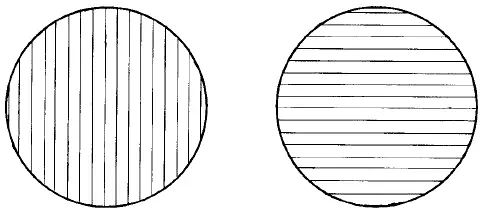
Рис. 202.. Какой кружок больше?

191. Обе дуги одинаковы.

192. Все полоски одинаковой длины.

193. Палубы у обоих кораблей имеют одинаковую длину.

194. Середина указана правильно.

195. Потому что они действительно равны.

196. Ошибки нет: фигура вокруг шляпы квадрат.

197. Прямая упрется в точку С.

198. Все три линии одинаковой длины.

199. Нет, не поместится.

200. Это тоже задача-ловушка. Кружки равны.

Данные относятся к 1924 г. — Прим. ред.

Данные относятся к 1924 г. — Прим. ред.

В издании Я. И. Перельман ВЕСЕЛЫЕ ЗАДАЧИ, Астрель, М 2003, другая иллюстрация — прим. верст.

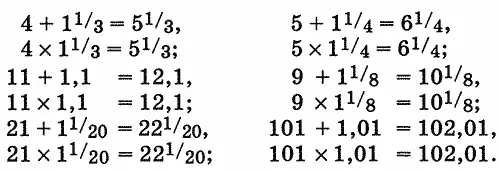
сантиметровой — прим. верст.

Козьмы Пруткова.

Точнее, не перегнать, а отстать, т. е. двигаться по поверхности Земли в сторону, обратную ее движению, так быстро, чтобы увеличить для себя продолжительность суток.

Человек может перегнать Землю и пешком — в 50 км от полюса.

Отсюда ясно, между прочим, что часто встречающееся в учебниках определение поверхности как «границы тела» несостоятельно; поверхность Мебиуса никакого тела ограничивать не может, а между тем это — поверхность..

Рис. 99 — прим. верстальшика

93 — прим. верст.

Водоизмещение корабля равно наибольшему грузу, который он может поднять (включая и вес самого судна). Тонна — около 60 пудов (1 пуд =16 кг. — Прим. ред.).

Я не сообщил этой цифры в условии задачи потому, что сама величина потери — 8-я, 10-я или 20-я часть — для решения задачи не имеет значения.

Для удобства их лучше наклеить на четыре стороны квадратного бруска.

Столько горошин помещается в кубическом сантиметре при рыхлой упаковке; при более же плотной укладке, когда часть горошины располагается в промежутке между соседними, горошин помещается больше.

Впрочем, полвека тому назад один английский учитель чистописания выполнил такую работу: он аккуратно расставил в толстой тетради миллион точек, по тысяче в каждой странице.

Эта задача заимствована из старинного русского учебника математики Ефима Войтяховского, изданного в конце XVIII века.