Александр Цветков - Язык программирования PASCAL

ProgramTable;

UsesCRT; // Подключение модулей

// Описания функций, требующихся в программе

functioncube(x:real):real; // возведение в куб

begin

cube:=x*x*x; // имени функции присваивается значение

end;

functionsign(x:real):integer; // вычисление знака числа

begin

ifx>0 thensign:=1

else ifx=0 thensign:=0

elsesign:=-1;

end;

// ==== Начало главной программы ==========

var a : real; // блок описания переменных

const a1 = -5.0; // блок описания констант (постоянных)

a2 = +5.0;

st = 0.5;

begin

a:=a1;

while(a<=a2) do

begin

writeln(a:4:1,cube (a):10:3,sign(a):3); // вызов функций

a:=a+st;

end;

end.

Обратите внимание, что внутри тела функции (заключенного в операторные скобки begin… end) вы обязаны хотя бы один раз имени функции присвоить значение. В этой программе также используется новый материал, не связанный с функциями, – это константы. Значение констант задается через знак равенства (а не присваивания). Тип константы определяется из типа присваиваемого значения. Константы, в отличие от переменных, не могут менять свое значение.

- 27 -

Рассмотрим еще один пример, в котором функция имеет два параметра разного типа.

ProgramPower2;

UsesCRT;

functionpower(x : real; n : integer) : real; // возведение в степень

var i : integer; // локальные переменные r : real;

begin

r:=1.0;

fori:=1 ton dor:=r*x; // накопление произведения

power:=r; // результат присвоить имени функции

end;

// ==== Начало главной программы ================

var i : integer; // блок описания переменных

begin

fori:=1 to10 do

writeln(i:2,power (2.0,i):6:0);

end.

В данном примере функция имеет два формальных параметра (типа real и типа integer), а также две локальных переменных. Имена локальных переменных действуют только внутри тела функции. Переменная i в главной программе, и переменная i внутри функции – это две разных переменных. При вызове функции первый фактический параметр соответствует первому формальному параметру. Второй параметр – второму.

Задание 9 1. Модифицируйте последний пример таким образом, чтобы функция power вычисляла правильно не только натуральные степени, но и отрицательные.

Напоминание:

x -n= 1 / x n.

Подсказка: следует использовать оператор if, а также функцию abs(n), которая вычисляет модуль числа.

(5 баллов)

2. Напишите функцию, вычисляющую факториал числа n! =1•2•3• ... •n.

Подсказка: ее несложно сделать, путем модификации функции power.

(5-8 баллов)

- 28 -

Для выполнения каких-либо действий (а не вычислений значений) существуют подпрограммы-процедуры. Они также могут принимать параметры, как и подпрограммыфункции. Давайте сразу проиллюстрируем работу процедуры на примере графической программы.

В стандартной графической библиотеке нет процедуры, рисующей треугольники. Давайте создадим такую процедуру и проверим ее работу.

ProgramUseProc;

UsesGraphABC;

Procedure Triangle(x1,y1,x2,y2,x3,y3:integer);

// Процедура рисует треугольник

begin

line(x1,y1,x2,y2);

line(x2,y2,x3,y3);

line(x3,y3,x1,y1);

end;

// Главная программа

begin

SetWindowSize(500,500);

Triangle(100,200,400,300,250,150);

Triangle(10,20,30,40,50,10);

end.

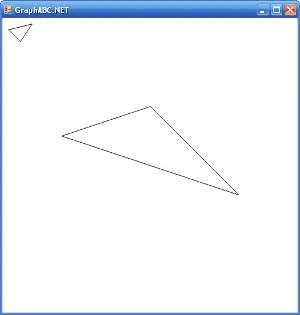
Как мы видим, процедура Trianlge имеет шесть целочисленных параметров и вызывает функции трижды функции Line для соединения точек. Создав такую процедуру, мы можем использовать ее столько раз, сколько нам надо в главной программе.

Задание 10

1. Создайте еще несколько новых графических процедур, которые бы расширили возможность стандартной библиотеки (ромб, параллелограмм, и т.п.) (по 3-4 балла за каждую)

- 29 -

Модули (Units)

Вы, наверное, обратили внимание на неудобство, связанное с тем, что все подпрограммы (как процедуры, так и функции) размещаются перед главной программой. Хотелось бы разместить их в отдельную библиотеку. Такая возможность есть, её предоставляют модули.