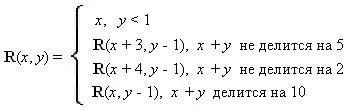Вячеслав Пупышев - 50 задач по началам программирования

X = 8

_____________________

Есть ли в заданном файле буква ы ?

ТЕХНИЧЕСКОЕ ЗАДАНИЕ.

Программа должна спросить имя файла и напечатать:

ДА - если в этом файле есть буква ы , и НЕТ - в про тивном случае.

ПРИМЕР.

Для текста задачи ответ: ДА .

Написать программу, которая запрашивает имя файла и пе чатает число, которое встречается в заданном файле чаще дру гих. Файл может содержать не только числа.

Длина чисел не имеет значения.

ПРИМЕР:

в последовательности 2 3 4 5 67 6 5 64 это число 6.

Написать программу, которая запрашивает имя файла и пе чатает длину самой большой последовательности из одного и

того же символа.

ПРИМЕР:

в тексте задачи самая длинная последовательность мм и длина ее 2.

В файле записано 10 символов. Записать их в другой файл в обратном порядке.

ПРИМЕР.

В файле: ротялипмоК

В файле с результатом: Компилятор

Задан текстовый файл из строк символов.

Написать программу, которая записывает исходный

файл в новый так, чтобы строки расположились в

обратном порядке.

ПРИМЕР.

для текста задачи получается:

обратном порядке.

файл в новый так, чтобы строки расположились в

Написать программу, которая записывает исходный

Задан текстовый файл из строк символов.

Решить уравнение: x + 2 • x + 3 • x + ...+ x • x = n . Вводится n , найти x . Какими могут быть n и x , догадайтесь сами.

ПРИМЕР.

n= 18

x=3

Решить уравнение: x !. N = y !. N - целое число. K ! [5] читается <���ка факториал> - определяется только для натуральных K . K ! = 1 . 2 . 3 . ... . K ,

0! = 1.

__________________________________

ТЕХНИЧЕСКОЕ ЗАДАНИЕ.

Получить для заданного N все различные пары ( x , y ).

ПРИМЕР.

N= 12

Ответ : (2,4)(11,12)

В кольце записаны N цифр, составляющих по часовой стрелке три числа: два слагаемых и сумму.

ТЕХНИЧЕСКОЕ ЗАДАНИЕ.

Написать программу, которая запрашивает строку цифр и, считая её кольцом, печатает какое-нибудь решение в виде A+B=C. Все цифры должны входить в числа в порядке следования в кольце. Цифр в кольце не более 100.

ПРИМЕР.

Ввод: 01902021

Вывод:190+20=210

Вычислить максимальное значение R ( x , y )для заданных целых x , y ( y<50 ).

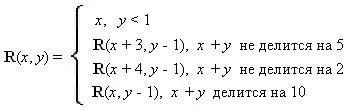
Внимание, «функция» R -неоднозначная (может давать разные значения на одинаковых аргументах).

ПРИМЕР.

X= 3

Y= 4

Максимальное значение R(3, 4)=16

Образец имеет вид:

образец ::=

::= |

::= '['']' |

::= <���символы>

Часть образца, заключенная в квадратные скобки показывает, что эту часть можно исключать. Таким образом, образец описывает множество строк. Образец всегда правильный. Например:

образец: [a[b]]c

описывает строки: a, ab, abc

Слово подходит под образец, если оно совпадает с одним из слов, описываемых образцом. Задача написать программу, которая по заданному образцу и слову печатает « НЕТ », если слово подходит под образец, и « ДА », если не подходит.

ПРИМЕР:

образец: [a[b]]c

слово: ab

ответ: ДА

Решить уравнение вида f(X) = A , где A - строка из маленьких латинских букв, X - переменная строка, f - функция на строках, построенная с помощью операций * и + над строками. Операция + обозначает конкатенацию [6] Т.е. сцепление строк, приписывание одной строки к другой. строк. Например, adbc + 123 = abcd 123. Результатом операции A * B будет стро ка, где после каждого символа A записана B ; если A или B - пустые строки, то результат будет также пустой строкой. На пример, ab * cd = acdbcd . Операции выполняются в порядке их следования.