Коллектив авторов - Метод. Московский ежегодник трудов из обществоведческих дисциплин. Выпуск 5 - Методы изучения взаимозависимостей в обществоведении

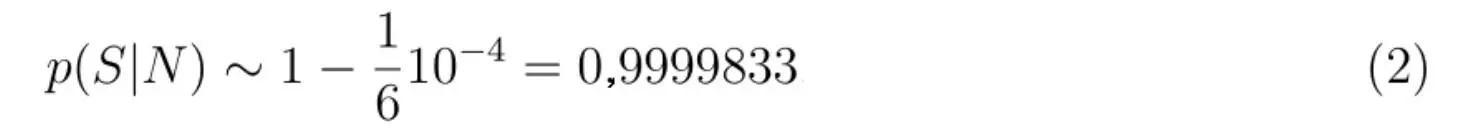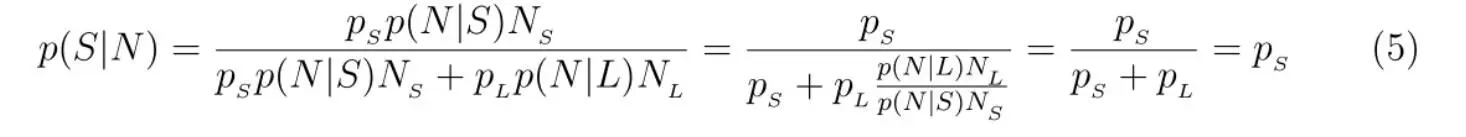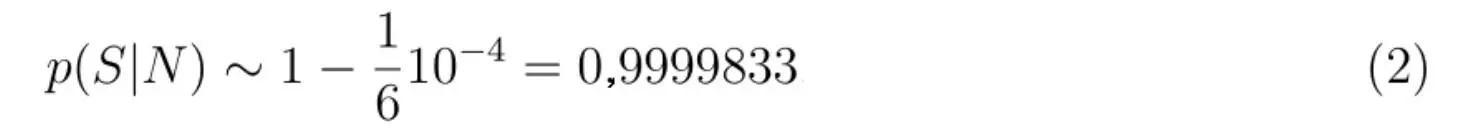
Другими словами, фактически со 100%-ной гарантией эти люди должны были оказаться правы в своих апокалиптических ожиданиях. Вероятность же текущего положения дел (на начало XXI в.) составила бы лишь 0,000017. Тем не менее, как мы знаем, именно это практически невероятное состояние человечества имеет место. Таким образом, древние люди совершили бы огромную ошибку, полагаясь на формулу (1). Но тогда почему мы должны доверять этой формуле?

B. Аргумент Doomsday дает заведомо неправильный ответ. Здравый смысл подсказывает, что вероятность p (S|N) должна быть равна просто p S. Очевидно, где‐то имеется ошибка в вычислениях.

Кен Олум утверждает, что знает где. Вот его рассуждения: для нахождения условной вероятности p (S|N) мы перемножили два числа (опуская нормировочный множитель):

p (S|N) ∼ p Sp (N|S), (3)

тогда как правильное выражение имеет вид

p (S|N) ∼ p Sp (N|S)N S. (4)

Вводя в (4) нормировочный множитель, имеем

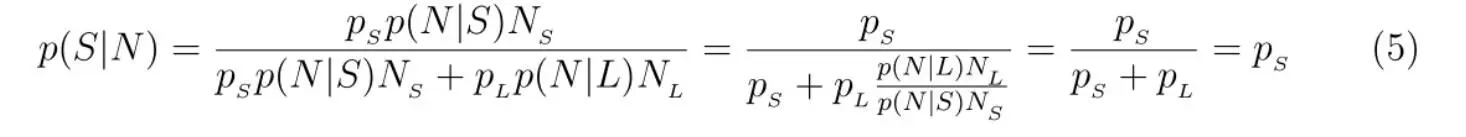
Ответ получается разумным, но почему нам следует использовать предписание (4), а не (3)? Согласно Олуму, для правильного вычисления p (S|N) необходимо перемножить три вероятности: вероятность того, что мы находимся в короткоживущей цивилизации (p S), условную вероятность того, что я N-й человек (p (N|S)), и p (N S|I) – условную вероятность того, что я нахожусь в короткоживущей цивилизации, при условии, что «я есть». Последнее выглядит странно и нуждается в пояснении. Суть дела в том, что сам факт моего существования служит аргументом в пользу того, что я нахожусь в долгоживущей цивилизации, насчитывающей большое число людей. Другими словами, вероятность p (N S|I) должна быть пропорциональна полному числу людей – N S. Для того чтобы сделать этот вопрос максимально ясным, рассмотрим (вслед за Кен Олумом) следующую гипотетическую игровую ситуацию. Пусть некое высшее существо (Олум называет ее богиней) имеет в запасе отель, содержащий 10 9одноместных номеров и такое же число людей (одним из которых являюсь я). Богиня бросает монету и в зависимости от того, что выпадает – «орел» или «решка», реализует следующую стратегию.

Стратегия 1.

1.1. Если выпадает «орел», то богиня случайным образом расселяет всех 10 9человек по номерам.

1.2. Если выпадает «решка», то богиня случайным образом выбирает 10 человек и наугад расселяет их по первым 10 номерам.

Предположим, что я обнаружил, что нахожусь в одном из первых 10 номеров. С какой вероятностью у богини выпал «орел»? Или иначе, какова вероятность того, что отель полон людей? Эти вопросы имеют прямое отношение к Аргументу Doomsday. В самом деле, результат, полученный по формуле (1), можно объяснить и так: если человечество будет существовать очень долго и полное число всех людей (N L) будет очень велико, то кажется весьма маловероятным найти себя в малой доле людей, живущих у истока цивилизации. Однако мы находим себя в нем, значит, полное число всех когда-либо живших людей, людей, живущих сейчас, и тех, кто будет жить после, не должно быть очень велико. Формула (1) просто дает количественное основание этой идеи. Аналогично в мысленном эксперименте Кен Олума кажется весьма маловероятным, что отель полон, коль скоро мы нашли себя уже в первой десятке номеров. Однако это интуитивно очевидное заключение оказывается неверным. Назовем группу людей, которых богиня будет расселять по номерам реферируемой группой. Теперь предположим, что монета упала «орлом». В этом случае с вероятностью единицы я окажусь в реферируемой группе. Вероятность же того, что богиня поместит меня в один из первых десяти номеров, составит 10 −8. Перемножая эти независимые вероятности, я получаю вероятность попасть в первые десять номеров при выпадении «орла», равной 10 −8. Если же монета упадет «решкой», то мои шансы попасть в реферируемую группу составят десять к миллиарду, зато вероятность того, что я окажусь в первой десятке номеров, равна, очевидно, 1. Перемножая эти числа, получаем ту же вероятность 10 −8, что и при выпадении монеты «орлом». Заметим, что вероятность моего попадания в реферируемую группу и есть величина p (N S|I) (или p (N S|I)). Отношение этих вероятностей в первом и втором случаях составляет один к 10 −8, т.е. равно отношению числа членов в реферируемых группах: 10 9к 10. Именно поэтому p (N S|I) ∼ N S, а p (N L|I) ∼ N L. Таким образом, вероятность моего попадания в номер, скажем, 7 не зависит от числа людей в отеле и составляет, очевидно, 10 –9. В свою очередь это означает, что вероятности выпадения монеты «орлом» или «решкой» равны, а значит, вероятность того, что отель полон, равна 1/2, т.е., возвращаясь к Аргументу Doomsday, p (S|N) = p S. Таким образом, парадокс Судного дня кажется решенным. Но не все так просто!