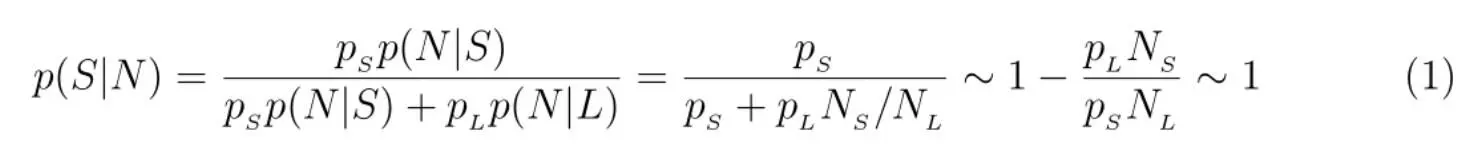Коллектив авторов - Метод. Московский ежегодник трудов из обществоведческих дисциплин. Выпуск 5 - Методы изучения взаимозависимостей в обществоведении

Все вышесказанное свидетельствует о кажущейся «непрактичности» космологии как физической дисциплины. Цель данной работы – опровержение этого утверждения. Мы попытаемся показать, что справедливо прямо обратное суждение: космология является самой практической из всех наук, поскольку, как мы увидим, приводит к выводам, весьма актуальным не только для космологов, но и для всех людей, в том числе далеких от науки. Мы покажем, что если так называемая стандартная космологическая модель (СКМ), о которой иногда говорят как о «космологическом коркодансе», верна, то человеческой цивилизации осталось существовать гораздо меньше, чем это принято думать! Насколько меньше? Речь идет не о миллионах или тысячах лет, а о столетиях или даже, при наиболее экзотичном варианте, десятилетиях! Вероятно, читатель подумает, что авторы занимаются мистификацией. Каким образом изучение вселенной как целого может привести к таким выводам? Поразительно, но может. Именно этой теме посвящена данная работа. Отметим, что предсказания о грядущем «конце света», сделанные на основе чисто статистических аргументов, давно и оживленно обсуждаются в литературе. Появился специальный термин: Аргумент Судного дня (в подлиннике Doomsday argument [Carter, 1983; Leslie, 1990; Gott, 1993; Nielsen, 1989]). Аргумент Doomsday не использовал космологических соображений и подвергался обширной критике. Наиболее ясно эта позиция изложена в статье Олума [Olum, 2002]. Мы, однако, покажем, что критика Олума несправедлива, если принять во внимание СКМ. Более точно, используя аргументацию Олума в рамках «космологического коркоданса», мы неизбежно приходим к справедливости Аргумента Doomsday. Другими словами, Кен Олум доказал справедливость Аргумента Судного дня, хотя и написал свою работу с целью опровержения последнего!

Работа организована следующим образом: во втором разделе мы обсуждаем Аргумент Судного дня и решение, предложенное Олумом для устранения последнего. В третьем разделе мы показываем, что правило подсчета частот в мультиверсе отличается от того, которое использовалось в [Olum, 2002] для решения парадокса Doomsday и, напротив, приводит к справедливости Аргумента Судного дня. В четвертом разделе, используя данные математической демографии и методы, развитые выше, мы оцениваем время наступления «конца света». Даже грубые вычисления свидетельствуют о том, что «конец света» должен наступить в течение ближайших десятилетий. Трудно счесть такое заключение чем‐то непрактичным, не так ли?

В своей классической постановке Аргумент Doomsday выглядит следующим образом: пусть p Sи p L – вероятности того, что человеческая цивилизация (раса) будет существовать соответственно «недолго» и «долго». Срок существования – не определяется. Все, что нам надо знать, – это то, что в первом случае человечество исчезнет, набрав в «общей сумме» N Sкогда-либо живших людей, а во втором – N L, причем N L>> N S. Разумеется, эта картина может показаться чрезвычайно упрощенной. Наверное, возможно множество вариантов развития человечества, и нелепо все сводить к двум возможностям. Тем не менее в качестве некоей усредненной картины ее использовать можно. Современный уровень знаний не позволяет вычислить числа p Sи p L= 1− p S, но этого и не требуется. Более того, можно даже принять оптимистичный взгляд на вещи и считать, что величина p Lпо крайней мере не меньше величины p S. Это не изменит конечного результата. Нас будет интересовать условная вероятность p (S|N), которая равна вероятности того, что «я» живу в короткоживущей цивилизации, при условии, что я N-й рожденный человек. Конечно, определить величину N – затруднительно, поскольку непонятно кого считать первым человеком. Но в принципе ясно, что какое бы соглашение относительно первого человека ни было принято, в рамках его число N будет определено.

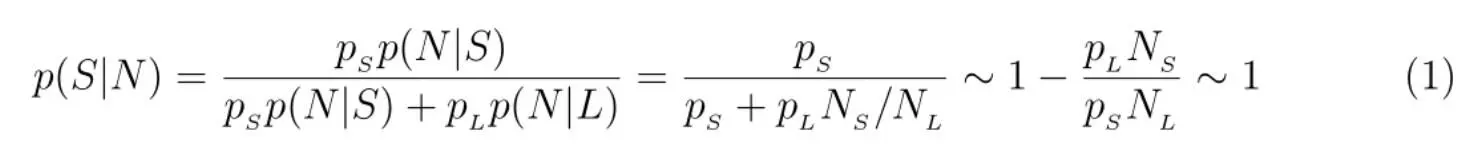
Пусть p (N|S) и p (N|L) условные вероятности того, что я N-й рожденный человек в, соответственно, короткоживущей и долгоживущей расах. Очевидно p (N|S)/p (N|L) = N L/N S. Используя формулу Байеса, находим результат, так как N S/N L<< 1. Таким образом, условная вероятность найти себя в короткоживущей расе неожиданно оказывается порядка единицы! Это и есть знаменитый Аргумент Doomsday.

A. Аргумент Doomsday содержит внутреннее противоречие. Представим себе, что несколько десятков тысяч лет назад численность народонаселения составляла в общей сумме (вместе с умершими) 1000 человек. Предположим, что эти люди – фаталисты, уверенные, что грядет конец света, и оценивают общее число всех людей своей расы, вплоть до этого конца в 10 6. Как мы знаем, сейчас число всех когда-либо живших людей составляет около 60 млрд человек 5 5 В пятом разделе мы поясним, откуда берется это число. . Примем, что p S= p L= 0,5. Тогда формула (1) дает