Владимир Кучин - Пирамида чисел Фибоначчи – Кучина. Научный комикс

Перед вами рисунок пирамиды чисел Фибоначчи – Кучина, на котором желтыми стрелками обозначены ступени ДЕСЯТИЧНОЙ ЛЕСТНИЦЫ. Да, автор не оговорился – и это существенное открытие в области науки о числах.

Мы строили левый и правый склоны пирамиды используя очень простые формулы сложения двух чисел для получения третьего (см. части 2—6). На левый склон пирамиды мы ставили числа из ряда Кучина, а на правый числа из ряда Фибоначчи.

И вот, числовая пирамида была достроена. Вертикальная формула построения пирамиды была понятна, но, оказывается, числа в пирамиде из ряда Кучина и ряда Фибоначчи СВЯЗАНЫ ГОРИЗОНТАЛЬНО ПО ДЕСЯТИЧНОЙ ПРОПОРЦИИ!!!

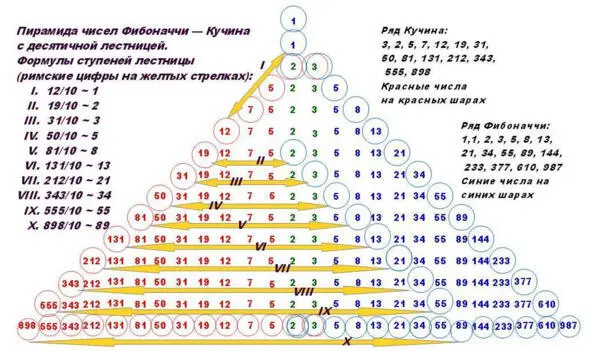
Иллюстрация «Лестница к Солнцу»

Формулы связи указаны на чертеже пирамиды. В данном случае число из ряда Кучина нужно разделить на 10 – это основание общепринятой десятичной системы – и округлить до целого.

Например, число из ряда Кучина «81» деленное на 10 дает «8,1» – округляем – «8». А это число из ряда Фибоначчи 8, которое стоит НА ЭТОЙ ЖЕ СТУПЕНИ ПИРАМИДЫ, ТОЛЬКО НА 10-й ПОЗИЦИИ СПРАВА. И так далее, все очень просто и весьма удивительно.

Так на Пирамиде чисел Фибоначчи – Кучина образовалась лестница из 10-ти ступеней, своеобразная «лестница к Солнцу», по которой можно подняться от подошвы пирамиды, от чисел «898 – 89», к ее вершине, числу «1». До числа «19» мы поднимемся без проблем, а от числа «12» к «1» залезем по желтой «альпинистской» веревке.

Представим себе, что мы виртуально стоим на вершине Пирамиде чисел Фибоначчи – Кучина и смотрим вокруг.

И, оказывается, что в окружающем нас мире числа из ряда Кучина, связанные удивительным десятичным соотношением с числами Фибоначчи, играют очень большую роль, они присутствуют в законах химии, физики, в природных явлениях, в скорости звука, в скорости света, в физических постоянных, в медицине, в геометрии.

Не пытаясь объять необъятное, расскажем о некоторых примерах «жизни» чисел из Пирамиды чисел Фибоначчи – Кучина в окружающем нас мире.

В последней статье – «Пирамида чисел Фибоначчи – Кучина. Лестница к солнцу» – автор показал, что пирамида чисел действительно существует, и обладает неожиданным десятичным свойством. Это свойство состоит в ДЕСЯТИЧНОЙ связи чисел ряда Кучина и чисел ряда Фибоначчи, что позволяет построить на пирамиде десятичные ступени.

Продолжим наши поиски и поговорим о ЗОЛОТОМ СЕЧЕНИИ. Этот термин имеет древнюю историю, в ней переплелись и математика и мистика и всякие оккультные идеи.

Автора в данном случае интересуют только факты. Поэтому обратимся к Большой Советской Энциклопедии, где прочитаем:

«ЗОЛОТОЕ СЕЧЕНИЕ, гармоническое деление, деление в крайнем и среднем отношении, деление отрезка АВ на две части т.о., что большая его часть АС является средней пропорциональной между всем отрезком АВ и меньшей его частью СВ ….

Алгебраич. нахождение 3.с. отрезка АВ = а сводится к решению уравнения… откуда х ~ 0,62.

Отношение х к а может быть также выражено приближённо дробями 2/3, 3/5, 5/8,

8/13, 13/21 и т. д., где 2, 3, 5, 8, 13, 21 и т. д.– Фибоначчи числа.»

Принято в честь древнегреческого архитектора Фидия обозначать число равное 1/х, где х – корень решения уравнения, о котором идет речь в энциклопедии, символом Ф.

С точностью до шести знаков после запятой Ф = 1,618034.

Множество материалов, написанных в основном в 19-м и начале 20-го века содержать сведения о РАЦИОНАЛЬНОМ ПРИБЛИЖЕНИИ к ЗОЛОТОМУ СЕЧЕНИЮ с помощью чисел Фибоначчи.

Самый доступный способ в этом убедиться – обратиться к Википедии по ссылке – https://ru.wikipedia.org/wiki/Золотое_сечение.

Автор статьи о ЗОЛОТОМ СЕЧЕНИИ в Википедии пишет:

«Рациональные приближения – 3/2; 5/3; 8/5; 13/8; 21/13; 34/21; 55/34; 89/55; … и. т. д. F {n+1} /F {n}, где F {n} – числа Фибоначчи (перечислено в порядке увеличения точности).»

А теперь пора обратиться к иллюстрации к нашей статье.

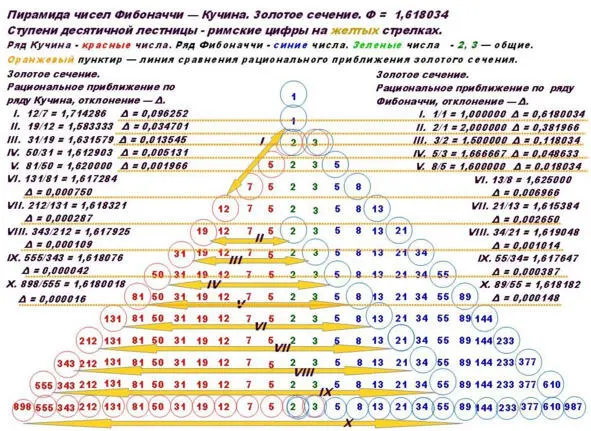
Иллюстрация «Золотое сечение»

Будет вести РАЦИОНАЛЬНОЕ ПРИБЛИЖЕНИЕ к ЗОЛОТОМУ СЕЧЕНИЮ по формуле, которую нам напомнил автор Википедии по числам ряда Кучина и ряда Фибоначчи, которые стоят на ДЕСЯТИЧНЫХ СТУПЕНЯХ пирамиды чисел.

Одновременно будем рассчитывать отклонения результата от числа Ф – числа Фидия.