Марат Авдыев - Восхождение к вершине гиперкуба. Великая теорема Ферма для миллиардов обычных людей

– Я тоже сталкивалась с подобным, – улыбаясь кивнула Татьяна. – причём, я спрашивала у тех собеседников, с которыми общалась: что Вы видите, можете ли Вы прочитать слайды нормально? – Отвечают, да, всё видим как обычно.

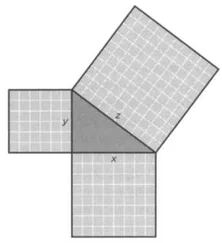
– Вот именно! – продолжал Борщов. – для того, у кого за спиной экран, изображение зеркальное, а для его собеседников – нет. Если оглянуться назад, через плечо, то слайды на большом экране, куда они проецируются, читаются, слайды и презентации на экране компьютера также читаются, а за спиной лектора – отражаются зеркально! В чем здесь фокус?

– На самом деле никакого фокуса нет, – подумав ответил Матвей, просто веб-камера, дисплей компьютера и программа вместе образуют своего рода электронное зеркало . Убедитесь в этом, посмотрите на нас вон в то зеркало.

– Ну и … – недоуменно пожал плечами Борщов, – зеркало, как зеркало.

– Вот именно так все мы привыкли видеть себя в отражении, и поэтому разработчики софта сделали всё таким образом, чтобы потакать нашим привычкам – пояснил Матвей.

– Я предлагаю сделать небольшой эксперимент, сказала Татьяна и начертила на двух салфетках трубочкой от коктейля, измазанной в шоколаде крупные буквы:

ДА

– А теперь, Артур, встань за спиной Александра Николаевича с этим транспарантом! – чуть повелительно сказала она своему брату.

Чувствуя значимость порученной миссии, Артур за спиной профессора поднял салфетку.

– Прочитайте, пожалуйста, Александр Николаевич, – обратилась она к Борщову, указывая на зеркало, где отражалось:

АД

– Ад! – прочитал Борщов, глядя в зеркало напротив столика.

– Представьте себе, что это слайды, – продолжала Татьяна. – Вы согласны, что происходит зеркальное отражение?

– Ну это очевидно! Но это почему мои собеседники читают все слайды нормально, а я – нет?

Татьяна жестом показала, что сейчас она всё объяснит и попросила Артура сесть напротив Борщова у свободного столика под зеркалом, держа в руках те же салфетки.

– Теперь снова ДА, прочитал Борщов.

– Александр Николаевич, – пришёл на помощь Матвей, – в мире программирования есть такая функция настройки дисплея, называется флип (flip) – отразить экран или фотографию. А вообще, программа может представлять изображение как угодно: прямо, зеркально, к верх ногами, под наклоном девяносто градусов и так далее. Но нам привычнее на экране читать тексты слева направо, а своё лицо видеть как в зеркале. Как бы Вы поступили на месте разработчиков зумпоподобных сервисов?

– Я бы… постарался сделать эффект полного присутствия – подумав немного ответил Борщов.

– Да, продолжила, Татьяна, поэтому свой текст на экране и своего собеседника мы видим без зеркального отражения, а изображение своей фигуры – как в зеркальном отражении. И всё что у нас за головой, попадающее в поле веб – камеры, мы также видим как в зеркале, посмотрите же на Артура ещё раз!

– Ах, да! – стукнул по своему столу Борщов. – ну какой я тупица! Это же надо, как просто! Коллеги, Вы меня положили на обе лопатки!

Ребята дружно улыбнулись, ещё бы: один гол в их пользу.

– Ну а теперь, я уверен, что с Теоремой Ферма Вы справитесь, – улыбаясь сказал Борщов. Что Вам удалось отыскать?

Матвей достал стопку листов с рисунками и стал пояснять. Он пытался разворачивать текст и рисунки к Борщову, но тот остановил репликой: я читаю вверх ногами без труда.

Матвей не торопясь начал:

– Давайте рассмотрим терему Ферма с позиции физики и геометрии. Именно в этом направлении есть шансы отыскать решение, основные идеи которого можно схематично уместить на достаточно широких полях книги.

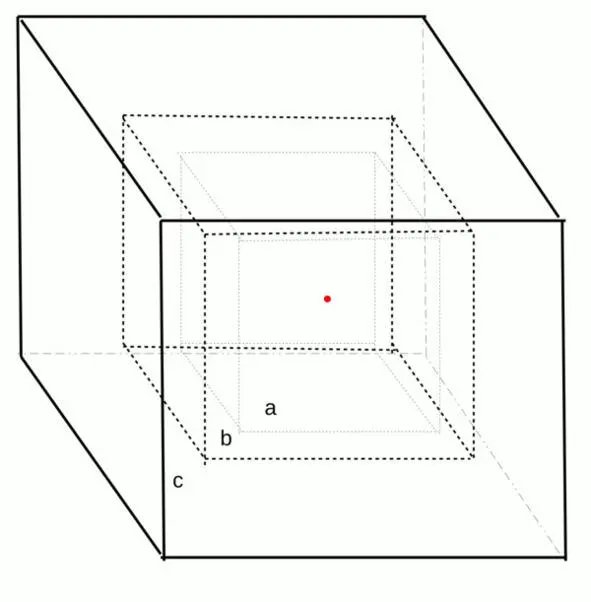
Рис. 2.1. Гиперкубы с ребрами a, b и c, вписанные друг в друга с общим центром, совпадающим с началом координат в пространстве размерности 3.

Не меняя общности, можно считать что справедливо неравенство для нашей тройки чисел a

На деле оказывается, что таким делителем всегда будет двойка и её степени, а это означает, что исходное предложение относительно числителя и знаменателя оказались ошибочными: оба они чётные, делятся на два, а мы исходно предполагали, что p, q не имеют общих делителей, которые заранее сократили.

Матвей говорил, водя карандашом по рисунку: