Александр Киселев - Математика шахматной доски

Итак, полимино – это клетчатый многоугольник, между любыми двумя клетками которого существует маршрут шахматной ладьи. Это не просто красивая связь с шахматами, а, видимо, самый наглядный способ объяснить школьнику, почему мы не рассматриваем фигурки, в которых клетки соединяются только вершинами.

Первый естественный вопрос, связанный с полимино, это их количество для каждого вида. То, что мономино всего одно, сомнений не вызывает. Как получить все варианты для домино? Достаточно добавить одну клетку к мономино. Легко увидеть, что во всех четырёх случаях получается одно и то же (с точностью до поворота), поэтому фигурка из двух клеток (домино) всего одна.

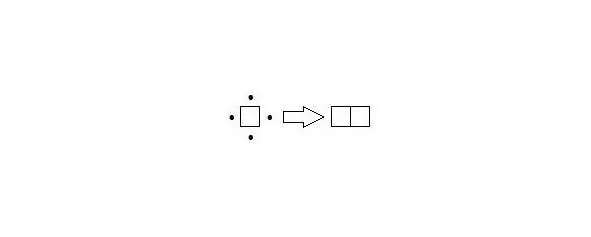
Рисунок 1. Получаем домино из мономино

Двигаясь дальше, выясняем, что тримино бывают уже двух видов: прямое и угловое.

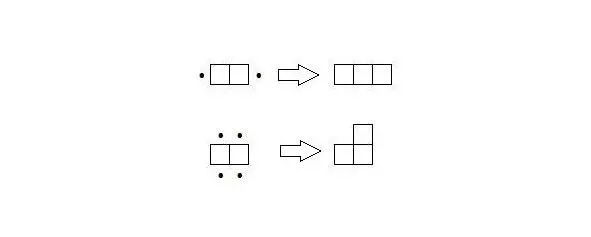
Рисунок 2. Получаем тримино из домино

Точно так же добавляем клетки и получаем пять различных видов тетрамино (см. рисунок 3) и 12 различных видов пентамино (это упражнение предлагается самостоятельно выполнить читателю, соответствующая картинка приведена в Приложении 2).

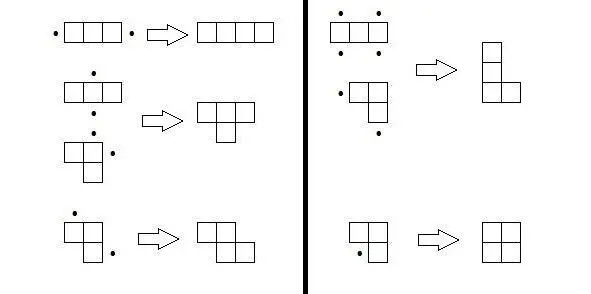
Рисунок 3. Получаем тетрамино из тримино

Тетрамино имеют устоявшиеся названия, которыми мы будем пользоваться в дальнейшем (на рисунке 3 слева направо и сверху вниз: прямое тетрамино, T-тетрамино, косое тетрамино, L-тетрамино и квадратное тетрамино).

Аналогично можно получать и все фигурки большего размера.

Достаточно естественным образом встаёт вопрос: из каких полимино можно составить доску? Чаще всего задача формулируется в другую сторону: на какие полимино можно разрезать всю доску (без остатка)? При этом слово «разрезать» здесь не следует трактовать буквально (хотя в моей практике был школьник, который именно так и поступал: брал бумажный квадрат 8×8 и резал его на заявленные части – однако даже к нему быстро пришло понимание, что результат такой работы будет практически невозможно продемонстрировать педагогу).

Ясно, что на мономино шахматная доска разбивается достаточно легко. Не вызывает особенных проблем и её разбиение на домино.

Рисунок 4. Разбиение на мономино

Рисунок 5. Разбиение на домино

Попытка разбить на прямые тримино приводит к тому, что остаётся одна клетка, не входящая ни в одну фигурку. Младшие школьники обычно либо в растерянности (им в принципе непривычно, что на вопрос «можно ли» бывает отрицательный ответ), либо говорят, что разрезать невозможно, потому что у них осталась одна лишняя клетка.

Школьник постарше, знакомый с понятием делимости, сразу формулирует это иначе: доску нельзя разрезать на тримино (хоть на прямые, хоть на угловые), потому что её площадь не делится на 3 (не делится без остатка , как принято называть это явление в школе 2 2 По поводу понятия делимости смотрите Приложение 3. ). Интересно, что на резонный вопрос «А почему она должна делиться?» некоторые из них ответить не могут, то есть это наблюдение настолько интуитивно очевидное, что далеко не всегда ребёнок задумывается над его причинами.

Итак, если шахматную доску (а, вообще говоря, любую клетчатую фигуру с целой площадью) можно разбить на полимино определённого вида (а, вообще говоря, на любые фигуры с целой площадью), то и площадь доски (большей фигуры) обязательно должна делиться на площадь этого полимино (меньшей фигуры). Более того, частное при этом делении равно количеству фигурок, получающихся при разрезании (это наблюдение пригодится нам в дальнейшем).

Условие делимости площадей является необходимым, то есть если площадь доски не делится на площадь маленьких фигурок, то разрезать точно не удастся. Обратное неверно!

Но для тримино всё работает идеально в нужную сторону: площадь шахматной доски (64 клетки) не делится на площадь тримино (3 клетки), поэтому её невозможно разрезать ни на прямые, ни на угловые тримино.