Яков Перельман - Головоломки и развлечения

— Древние думали, что, когда пути лабиринта достаточно хорошо запутаны, выбраться из них совершенно невозможно. Однако это не так. Можно доказать с математической достоверностью, что безвыходных лабиринтов устроить нельзя. Мало того: не только из всякого лабиринта можно найти выход, но можно обойти все его закоулки, ни одного не пропустив, и все-таки потом благополучно из него выбраться. Надо только взяться за дело, придерживаясь строгой системы, и притом с известными предосторожностями. 200 лет назад французский ботаник Турнефор отважился посетить на острове Крит одну пещеру, о которой существовало предание, что благодаря бесчисленным своим переходам она представляет безвыходный лабиринт. Таких пещер на Крите несколько, и возможно, что они-то и породили в древности легенду о лабиринте царя Миноса. Как же поступил французский ботаник, чтобы не заблудиться? Вот что рассказывает об этом его соотечественник, математик Люка.

Брат взял с этажерки старую книгу под заглавием «Математические развлечения» и прочел вслух следующее место, которое я потом переписал:

— «Побродивши некоторое время со своими спутниками по целой сети подземных коридоров, мы подошли к длинной и широкой галерее, которая привела в обширную залу в глубине лабиринта. Мы сделали, — говорит Турнефор, — в полчаса 1460 шагов по этой галерее, не уклоняясь ни вправо, ни влево… По обе стороны от нее тянется столько коридоров, что в них непременно запутаешься, если не принять необходимых предосторожностей; а так как у нас было сильное желание выбраться из этого лабиринта, то мы и позаботились обеспечить себе обратный путь.

Во-первых, мы оставили одного из наших проводников у входа в пещеру и велели ему тотчас же собрать людей из соседней деревни для нашего освобождения, если мы не вернемся к ночи. Во-вторых, у каждого из нас в руках было по зажженному факелу. В-третьих, на всех поворотах, которые нам казалось затруднительным отыскать впоследствии, мы прикрепляли справа к стене нумерованные бумажки. И, в-четвертых, один из наших проводников клал по левую сторону заготовленные им заранее пучки терновника, а другой посыпал дорогу рубленой соломой, которую он все время нес с собой в мешке».

— Все эти хлопотливые предосторожно-сти, — сказал брат, когда кончил чтение отрывка, — не так необходимы, как тебе, быть может, кажется. Во времена Турнефора, впрочем, иначе и нельзя было поступить, потому что тогда еще задача о лабиринтах не была разрешена. В наши дни выработаны правила странствования по лабиринтам, менее обременительные, но не менее надежные, нежели предосторожности французского ботаника.

— Ты знаешь эти правила?

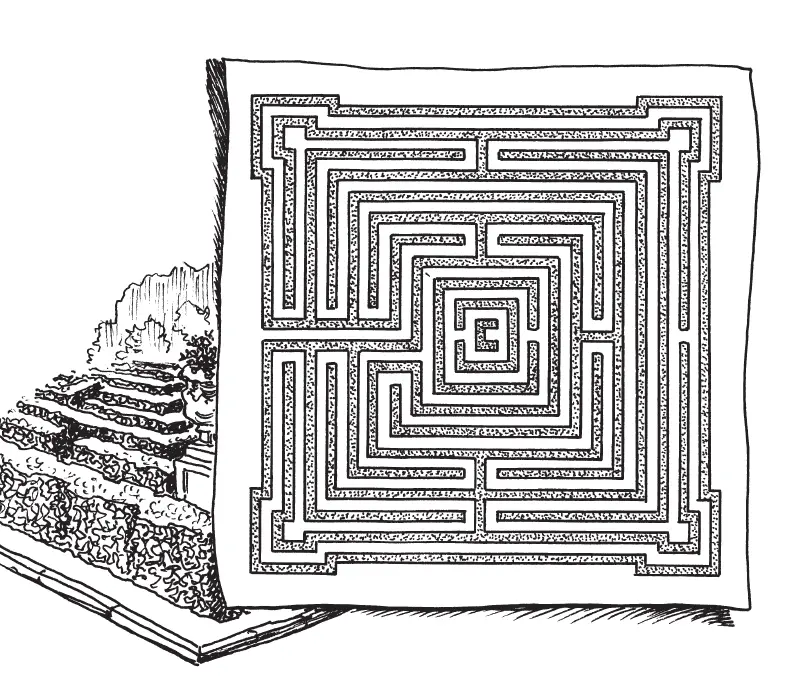
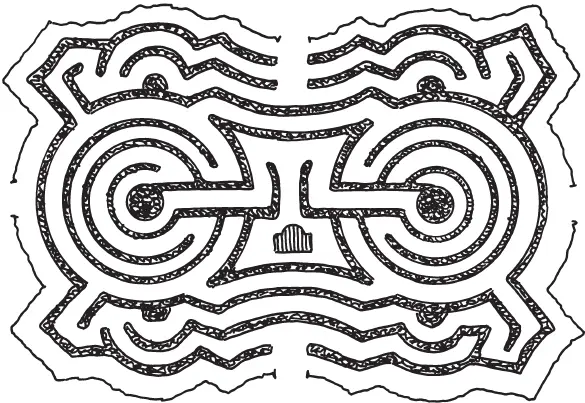
— Они несложны. Первое правило состоит в том, что, ступив в лабиринт, идут по любому пути, пока не зайдут в тупик или к перекрестку. Если пришли в тупик, возвращаются обратно, и два камешка у выхода из него будут показывать, что этот коридор пройден дважды. Если же приходят к перекрестку, то идут далее по любому коридору, отмечая камешком всякий раз путь, по которому прибыли, и путь, по которому отправляются далее. Таково первое правило. Второе гласит следующее: прибыв по новому коридору на такой перекресток, на котором уже побывали раньше (это видно по камешкам), тотчас же идут назад, положив у конца коридора два камешка. Наконец, третье правило требует, чтобы, придя на посещенный уже перекресток по коридору, также уже раз пройденному, отметить путь вторым камешком и идти по одному из тех коридоров, по которому еще ни разу не шли. Если такого не оказывается, выбирают коридор, у входа в который лежит всего один камешек (то есть коридор, пройденный всего один раз). Придерживаясь этих трех правил, можно обойти дважды, то есть туда и назад, все коридоры лабиринта, не пропустив ни одного закоулка, и благополучно выбраться на свободу. У меня имеется несколько планов лабиринтов, которые я вырезал в разное время из иллюстрированных журналов. Если хочешь, можешь попытаться совершить по ним путешествие. Надеюсь, что после всего того, что ты уже знаешь, тебе не грозит опасность заблудиться в них. А если у тебя много терпения, можешь на деле осуществить подобный лабиринт — хотя бы Гемптон-Кортский, о котором писал Джером, — соорудив его с твоими товарищами на нашем дворе из снега.