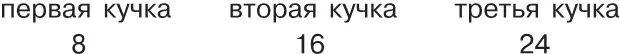Яков Перельман - Головоломки и развлечения

Спрашивающий должен брать всегда нечетное число спичек. Этим он обеспечивает своему партнеру проигрыш во всяком случае — положит ли тот две или одну спичку. Действительно:

нечетное число + 1 = четному числу,

нечетное число + 2 = нечетному числу,

то есть в обоих случаях получится противоположное тому, что было указано партнером.

В этой игре участвуют двое. На стол кладется кучка из 20 спичек, и играющие, один после другого, берут из этой кучки не более трех спичек каждый. Проиграет тот, кто берет последнюю, и, значит, выигрывает тот, кто оставляет противнику всего одну спичку.

Как должны вы начать игру и вести ее дальше, чтобы наверняка выиграть?

Желая выиграть, вы должны начать с того, что берете три спички. Из оставшихся 17 противник ваш может взять одну, две или три спички, по своему желанию, оставив в кучке 16, 15 или 14 спичек. Сколько бы он ни взял, вы следующим ходом (беря три, две или одну спичку) оставляете ему 13 спичек. Дальнейшими ходами вы должны оставить в кучке последовательно девять, пять и, наконец, одну спичку, то есть выигрываете.

Говоря короче: вы берете в начале игры три спички, а в дальнейшем каждый раз столько, чтобы ваша взятка вместе с предыдущей взяткой партнера составляла четыре спички.

Этот план игры найден следующим рассуждением: вы всегда сможете оставить противнику одну спичку, если предыдущим ходом оставили ему пять (тогда, сколько бы он ни взял — три, две, одну, — останется две, три, четыре, то есть благоприятное для вас число спичек); но, чтобы иметь возможность оставить пять, вы должны предыдущим ходом оставить девять, и т. д. Так, «пятясь назад», легко рассчитать все ходы.

Это задача-шутка, довольно забавная. На столе лежат три спички. Не прибавляя и не ломая ни одной спички, сделайте из этих трех спичек четыре.

Вы делаете «четыре» — просто четыре, а не четыре спички — следующим образом:

Таким же незамысловатым, но для многих неожиданным способом вы могли бы сделать из трех спичек шесть (VI), из четырех — семь (VII) и так далее.

Вот еще образчик задачи-шутки подобного же рода:

3+2 = 8!

На столе лежат три спички. Прибавим к ним еще две — и получите… восемь!

И здесь выручает римская нумерация. Вот ответ: III + II = VIII.

3 + 2 = 8

На столе лежат 48 спичек, распределенных по трем кучкам. Сколько спичек в каждой кучке, вы не знаете. Зато вы знаете следующее: когда из первой кучки переложили во вторую столько, сколько в этой третьей имелось, и, наконец, из третьей в первую столько, сколько в этот момент в кучке имелось, то во всех трех кучках оказалось спичек поровну.

Можете ли вы сказать, сколько спичек было в каждой кучке первоначально?

Задачу нужно решать с конца. Нам говорят, что после всех перекладываний число спичек в кучках оказалось одинаковым. Так как от этих перекладываний общее число спичек во всех трех кучках не изменилось и, значит, осталось прежнее (48), то в каждой кучке после трех перекладываний оказалось по 16 спичек. Следовательно, к концу имеем:

Непосредственно перед этим в первую кучку было прибавлено столько, сколько в ней имелось, то есть число спичек в ней было удвоено. Значит, до последнего перекладывания в первой кучке было не 16, а восемь спичек; в третьей же кучке, откуда эти восемь спичек были взяты, имелось 16 + 8 = 24.

Теперь у нас такое распределение спичек:

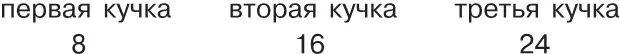
Далее, мы знаем, что перед этим из второй кучки было переложено в третью столько спичек, сколько имелось в третьей кучке. Значит, 24 — это удвоенное число спичек, бывших в третьей кучке до второго перекладывания. Отсюда узнаем распределение спичек после первого перекладывания:

Легко сообразить, что раньше первого перекладывания, то есть до того, как из первой кучки было переложено во вторую столько спичек, сколько в этой второй имелось, распределение спичек было такое: