Далее учитель открывает на доске другие примеры для 2-й команды.
Игра продолжается аналогично. Подводятся итоги соревнования.
5. Где произойдет стыковка космических кораблей?
Дидактическая цель. Формировать вычислительные навыки.
Содержание. В космос в заданном направлении запущены 3 космических корабля. Каждый ряд составит экипаж корабля. Поведут корабли 3 летчика-командира (3 ученика от каждой команды поочередно). Все другие ученики — помощники командира. Каждый корабль летит в заданном направлении. Его путь зашифрован примерами, выше которых записаны ответы, один из них. определяет направление данного корабля. Необходимо показать стрелками правильный путь полета каждого космического корабля. В заданном направлении корабли стыкуются, стрелками надо показать, где они встретятся. Если вызванные ученики (командиры) будут ошибаться, то члены экипажа должны исправлять ошибки своего командира. Полет покажет, кто станет настоящим командиром. Учащиеся от каждой команды выходят поочередно к доске и решают по одному примеру.
Побеждает тот экипаж, который не допустит ни одной вычислительной ошибки и правильно определит место стыковки космических кораблей.
Приведем схему полета космических кораблей.
I экипаж (1-й ряд) II экипаж (2-й ряд) III экипаж (3-й ряд)
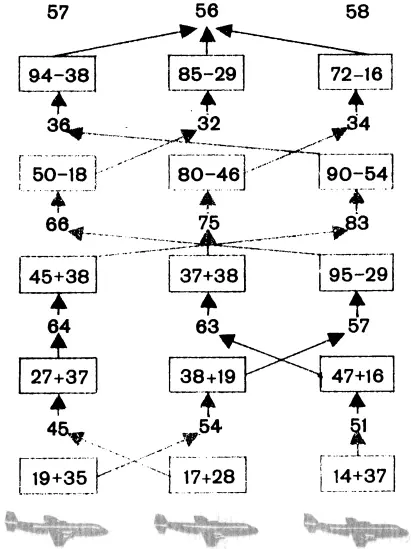
6. На какой час назначен сбор?
Дидактическая цель. Обучать учащихся приему самостоятельного нахождения правила, по которому записаны числа.
Оборудование. Рисунок ромашки, на которой записаны числа.
Содержание. Командир одной октябрятской звездочки решил назначить время ее сбора с помощью игры. Он засекретил его, записав на цветке ромашки числа, и предложил самим догадаться о времени сбора и записать его в середине рисунка. С этой целью они должны проследить за изменением чисел, записанных на лепестках
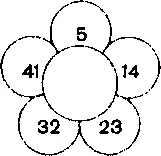
ромашки. Начиная с числа 5 по часовой стрелке, найти число, с помощью которого изменяются все числа. Оно и будет обозначать время сбора октябрятской звездочки. Дети из соседнего класса догадались. А вы сможете узнать время сбора октябрятской звездочки?
7. По какой тропинке ты пойдешь?
Дидактическая цель. Систематизировать и обобщать знания учащихся по различным разделам программы.
Содержание. Октябрята на выходные дни вместе с учительницей решили отправиться на туристическую базу пешком через лес. К ней вели две тропинки. Учительница узнала, что одна из них после дождя затоплена водой. Чтобы предупредить об этом ребят, она предложила им игру-загадку: догадаться по цепочкам примеров, по какой из тропинок связь с туристической базой не нарушена (по какой из них можно пройти успешно). Она зашифровала каждую тропинку цепочкой примеров такого вида:

Октябрята сразу догадались, по какой тропинке они пойдут на туристическую базу. А вы догадались?
8. Волшебная таблица
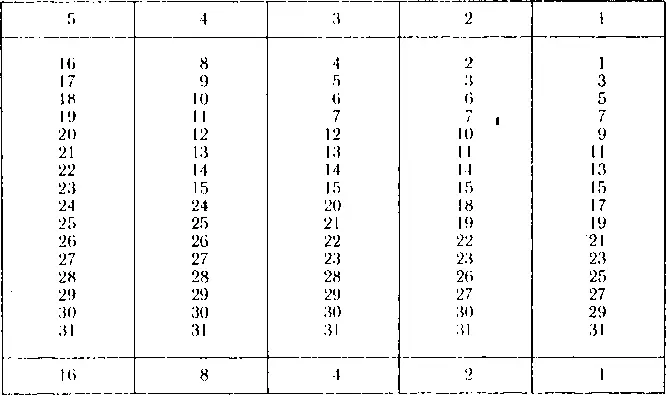
Содержание.
1. Учащиеся задумывают какое угодно число (не больше 31) и указывают, в каких столбиках этой таблицы находится задуманное число, а один из учеников отгадывает. Для отгадывания задуманного числа он складывает числа, записанные в конце каждого столбика в тех графах, где оно находится. Например: один из учеников задумал число, находящееся в четвертом и пятом столбиках. Сложив нижние числа в них (16+8), ученик отгадывает задуманное число 24.
2. Учитель задумывает число и называет номера столбиков, в которых оно находится. Дети, сложив последние (нижние) числа в этих столбиках, отгадывают это число и показывают его на кар* точках с цифрами учителю.
9. Математический телефон (II вариант)
Дидактическая цель. Формировать вычислительные навыки.
Содержание. Идет соревнование по рядам. Каждому ученику, сидящему за первой партой, учитель называет однозначное число шепотом, чтобы не слышали другие ученики класса. Далее учитель показывает на следующие схемы:
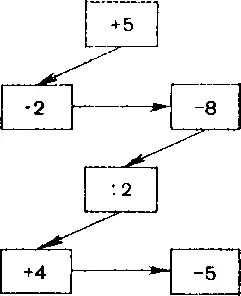
Учитель называет шести ученикам, сидящим за первыми партами, числа: 2, 3, 4. Он показывает на первый прямоугольник, все ученики, получившие от учителя числа, прибавляют к нему число 5, затем поворачиваются к ученикам, сидящим за ними, называют им результат. Далее учитель показывает на следующий прямоугольник, ученики, сидящие за второй партой, производят действие умножения на 2 и тихо называют ответы ученикам, сидящим за ними, и т. д. Игра продолжается до тех пор, пока ученики не выполнят всех действий по схеме. Сидящие за первыми партами выполняют роль контролеров. Они выполняют всю цепочку действий. В конце соревнования ученики, сидящие за последними партами, должны записать окончательные ответы, а сидящие за первыми — утвердить их или отвергнуть.
Читать дальше

















