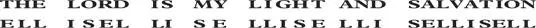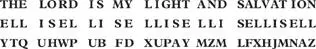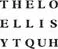Philip Kerr - Dark Matter

Over the next few weeks Newton continued to make only slow progress with the cipher, which moved me to suggest, when we were in the office one day, that he might seek the help of Doctor Wallis of Oxford. But Newton treated my suggestion with scorn and derision.

“Ask help of Wallis?” he said with incredulity, as he set to stroking the cat. “I should sooner solicit the opinion of Melchior. ’Tis one thing to borrow a man’s books, but quite another to make use of his brains. Go to him, cap in hand, and confess that I am baffled by this cipher? Why, then the man would bend Heaven and Earth to do something which I could not; and, having done so, would tell all the world. I would never hear the end of it. It would be better that I stuck a bare bodkin in my own side than let him put a thorn there to plague me with.”

Newton nodded angrily. “But it is right that you hold this up to me, for it serves to prick my thinking parts toward the devising of the solution of this conundrum. For I’ll not be dunned like some vulgar arithmetician who can practice what he has been taught or has seen done but, if he is in error, knows not how to find it out and correct it; and if you put him out of his road, he is at a complete stand.

“Yes sir, you encourage me, by God you do: to reason nimbly and judiciously about numerical frequency, for I swear I shall never be at rest till I get over every rub.”

Thus I observed that the cleverer the person, the more certain is his conviction that he is able to solve a puzzle which nobody else can solve; and that this goes to show the truth of Plato’s theory that knowledge involves true belief but goes beyond it.

After that, Newton was almost never without a black lead and a sheet of paper that was covered with letters and algebraic formulas, with which he strove to work out the cipher’s solution. And sometimes I altogether forgot that he did this work. But I well remember the time when Newton finally broke the code. All of a sudden there was great talk of a peace with the French near signing. Formal negotiations between ourselves and the French had been under way since May, at the Dutch town of Rijswijk. This was just as well, for it was common knowledge that the fleet was in a dreadful parlous state at anchor in Torbay, for want of provisions that was occasioned by the severe lack of good money. It was even said by my brother Charles that we had borrowed Dutch money to pay English sailors, and if so, then it’s certain nothing but a peace could have retrieved our situation.

The date was August the twenty-seventh, 1697, and I can still recall how I was a little surprised when Newton ignored my news of the peace and instead informed me, most triumphantly, that the deciphering of the letters was done and immediately made pertinent sense.

I accepted his word on the matter straightaway — for there was no denying the look of immense satisfaction on his face — and congratulated him most warmly upon the solution; and yet he still insisted on demonstrating the ingenious construction of the cipher in order that I might be satisfied of the truth of what he said. Newton drew his chair up to our table in the Mint office and, pushing Melchior away from his papers, showed me the many pages of his copious workings.

“In truth,” he explained, with much excitement, “a brief glimpse of how I might solve it presented itself to my mind just a few days ago, but only very vaguely. But now I see that it is all to do with constants and functions, which is but a cruder system of my own fluxions.

“The code is based in part on a system that uses a single short and repeating word, known to both correspondents, as the key to the cipher. Let us say that the keyword is your own surname. The encipherer repeats this keyword beneath his message, thus.” Newton wrote two lines of text on a sheet of paper:

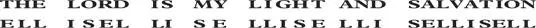
“Observe,” he continued, “how all the letters of the alphabet have a numerical value from one to twenty-six.”

“The letter T in our message is the twentieth letter in the alphabet,” he said. “We add this to the key letter that appears below. This is an E and the fifth letter in the alphabet. The sum of these two letters is twenty-five, which is the letter Y . This becomes the first letter of our cipher. Of course the sum of two letters may easily be more than twenty-six, for instance with the letters T and 5. Their sum is thirty-nine. Therefore, in order that we do not run out of cipher letters, we start the alphabet again so that after the letter Z , which is worth twenty-six, the letter A becomes worth twenty-seven, and so on. In this way, thirty-nine gives us the cipher letter M . When it is finished, the whole message in cipher would read as follows.”

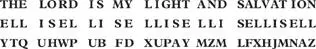
“The person wishing to decipher the message,” continued Newton, “executes the procedure in reverse. He writes out the cipher with the key word repeating underneath, and subtracts their numerical values. E , worth five, is subtracted from Y , worth twenty-five, which gives us twenty. Twenty-six is then added, to take account of any minus numbers. This gives us forty-six and the letter T . Equally, if we look at the cipher word XUPAY , we see that if we subtracted our keyword letter S from the cipher letter A , we would end up with one minus nineteen, which gives us minus eighteen. Minus eighteen plus twenty-six is worth eight, which gives us the letter H , from the message word LIGHT. ”

I nodded as, slowly, I began to understand the character of the cipher he described.

“As I said to you before,” explained Newton, “the code we have been dealing with here in the Tower is based on this general principle of a repeating keyword. But this makes it most susceptible to solution, for the key is always in full view of him who would make the decipherment. For example, you may perceive that in the cipher the letter X occurs twice in the cipher, and both times it conceals the same message letter L . Similarly the letter U occurs three times, and twice it conceals the message letter I . And it can be observed that one quarter of the time, common fragments such as the ‘TH’ in ‘THE’ will correspond exactly to ‘EL’ in ‘ELLIS.’ This is the weakness inherent in the system.

“Therefore the person who devised this key added an ingenious and numerical force that produced a motion within the key to hide those common fragments much more effectively. And yet so simple too, for the keyword itself changes based on the message, in a simple series progression. In this system, the keyword becomes a function of the letter L .

“The first five letters of the message would be encrypted in the normal way.”

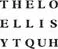
“But for the next five letters, the key changes based on the five encrypted letters — Y,T,Q,U , and H — according to whether or not the letters of the encryption appear before or after L . Any encrypted letters between M and Z cause the keyword to be incremented by one letter. But any letters before or including L cause the requisite letter of the keyword to remain the same. Or, to put it another way, Ato L are our constants, while M to Z are our variables. For example, with:”