Стивен Прата - Язык программирования C. Лекции и упражнения (6-е изд.) 2015

typedef struct pair {

Trnode * parent;

Trnode * child;

} Pair;

Функцию Seekltem() можно реализовать рекурсивно. Однако чтобы ознакомить вас с разными приемами программирования, для нисходящего обхода дерева мы применим цикл while. Подобно AddNode(), для навигации по дереву функция Seekltem() использует ToLeft() и ToRight(). Первоначально Seekltem() устанавливает указатель look.child так, чтобы он ссылался на корень дерева, а затем, по мере прохода по пути к возможному местонахождению элемента, переустанавливает этот указатель на последующие поддеревья. Одновременно указатель look.parent устанавливается для ссылки на последующие родительские узлы. Если подходящего элемента не найдено, значением указателя look, child будет NULL. Если искомый элемент находится в корневом узле, look.parent равно NULL, т.к. корневой узел не имеет родительского узла. Ниже приведен код функции Seekltem().

static Pair Seekltem(const Item * pi, const Tree * ptree)

{

Pair look; look.parent = NULL; look.child = ptree->root; if (look.child == NULL)

return look; /* преждевременный возврат */ while (look.child != NULL)

{

if (ToLeft (pi, & (look.child->item) ) )

глава 17

{

look.parent = look.child; look.child = look.child->left;

}

else if (ToRight(pi, &(look.child->item)))

{

look.parent = look.child; look.child = look.child->right;

}

else /* если элемент не расположен ни слева,

ни справа, он должен быть таким же */ break; /* look.child - это адрес узла, содержащего элемент */

}

return look; /* возврат в случае успеха */

}

Обратите внимание, что поскольку функция Seekltem() возвращает структуру, ее можно применять с операцией членства в структуре. Например, в функции Addltem() используется следующий код:

if (Seekltem(pi, ptree).child != NULL)

При наличии Seekltem() написание кода функции InTree() открытого интерфейса не составит труда:

bool InTree(const Item * pi, const Tree * ptree)

{

return (Seekltem(pi, ptree).child == NULL) ? false : true;

}

Соображения по поводу удаления элемента

Удаление элемента представляет собой наиболее трудоемкую задачу, т.к. необходимо заново соединить остающиеся поддеревья для формирования допустимого дерева. Прежде чем приступить к программированию решения этой задачи, имеет смысл визуально представить действия, которые должны быть предприняты. На рис. 17.13 иллюстрируется простейший случай. Здесь удаляемый узел не имеет дочерних узлов.

Расширенное представление данных 773

Такой узел называется листом. В этом случае понадобится только переустановить указатель в родительском узле в NULL и с помощью функции free() освободить память, занимаемую удаленным узлом.

Следующая по сложности задача — удаление узла с одним дочерним узлом. Удаление узла ведет к отделению дочернего поддерева от остального дерева. Для исправления такой си туации адрес дочернего поддерева должен быть сохранен в родительском узле в позиции, которая ранее была занята адресом удаленного узла (рис. 17.14).

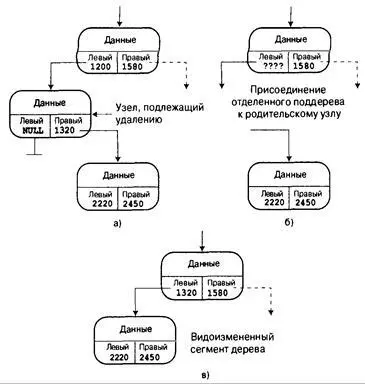
Рис. 1 7.14. Удаление узла с одним дочерним узлом

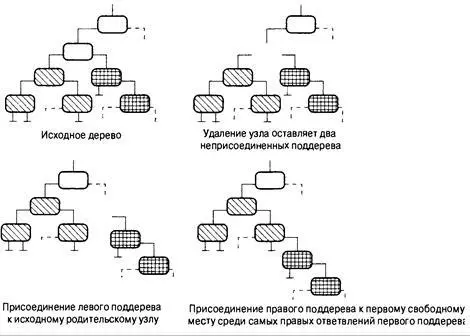
Последний случай связан с удалением узла, имеющего два поддерева. Одно поддерево, скажем, левое, может быть присоединено к тому узлу, к которому вначале был присоединен удаленный узел. Но куда поместить оставшееся поддерево? Вспомним базовый принцип формирования древовидной структуры. Каждый элемент в левом поддереве предшествует элементу в родительском узле, а каждый элемент в правом поддереве следует за элементом в родительском узле. Эго означает, что каждый элемент в правом поддереве расположен в структуре дальше любого элемента из левого поддерева. Кроме того, поскольку правое поддерево ранее было частью поддерева, начинающегося с удаленного узда, каждый элемент в правом поддереве предшествует родительскому узлу удаленного узла. Вообразите себе спуск по дереву в поисках позиции для помещения начала правого поддерева. Он предшествует родительскому узлу, поэтому далее необходимо следовать вниз по левому поддереву. Однако начало поддерева должно быть расположено после всех элементов в левом поддереве, поэтому необходимо последовать правой ветвью левого поддерева и выяснить, имеется ли в ней место для нового узла. Если нет, потребуется продолжать спуск по правой ветви

774 глава 17 левого поддерева до тех пор, пока свободное место не будет найдено. Этот подход продемонстрирован на рис. 17.15.