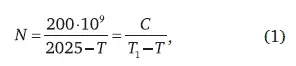Сергей Капица - Парадоксы роста. Законы глобального развития человечества

Для представления различных стадий роста и развития во времени полезно анализировать рост в разных масштабах, обращаясь к такой «лупе времени». (Ср. рис. 2, 5, 7, 8, 9, 18 и табл. 1.)

В заключение заметим, что помимо фундаментального значения таких работ для понимания развития человечества в целом подобные исследования глобальной истории необходимы и для осмысления судеб нашей страны. Благодаря географической протяженности, истории и разнообразию социальных и экономических условий Россия во многом воспроизводит глобальные процессы. Поэтому с учетом исторических масштабов этих проблем для нас существенно их понимание на уровне всего человечества, что дает возможность по-новому обратиться и к российским проблемам в критическую эпоху мировой истории.

Таким образом, предложенное новое видение прошлого основано на количественном подходе к антропологии и истории. В то же время эти представления затрагивают фундаментальные глобальные проблемы и обоснования экономики, а критерии устойчивости развития связаны с вопросами мировой безопасности. В частности, это открывает путь для понимания того системного социально-экономического кризиса, который так внезапно пришел и столь стремительно развивается в мире.

Ответ на центральный вопрос – чем человек обязан своему развитию, в результате которого его численность на пять порядков превосходит всех сравнимых с ним тварей, – как антропология, так и история связывают с сознанием человека. Однако для автора задача состоит в том, чтобы выразить этот вывод на языке физических теорий и математических моделей, которые опираются на основные представления, принятые в науках об обществе и человеке.

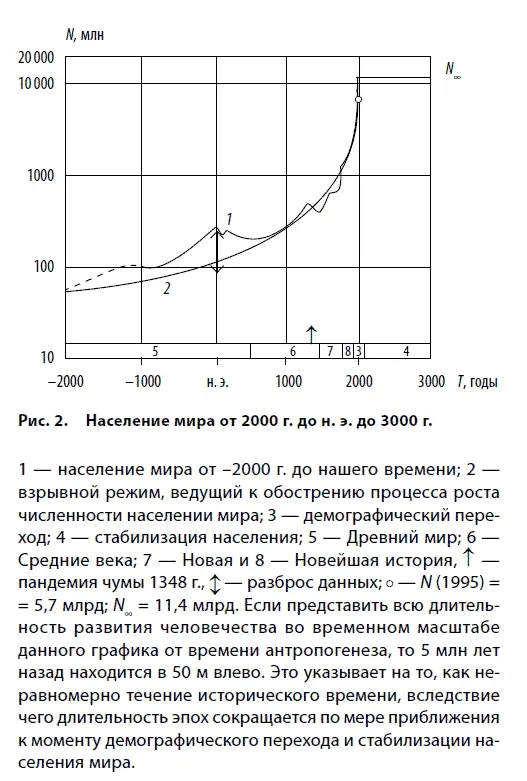
Для описания роста человечества рассмотрим три основные траектории развития (рис. 3). Первым показан линейный рост А, где численность населения N растет пропорционально времени T и скорость роста постоянна. График линейного роста лучше всего отображать на линейной сетке для времени и численности населения. При экспоненциальном росте Вскорость уже пропорциональна самой численности населения и в этом случае появляется характерное время для роста. В математике обычно принято обращаться ко времени T Еэкспоненциального роста системы в е раз, где е = 2,72 – основание натуральных логарифмов. Часто прибегают к более наглядному времени удвоения T 2= T Еln2 = 0,7 T Екоторое на 30 % меньше T Е.

Экспоненциальный рост отображается прямой на полулогарифмической сетке, на которой время T представлено на линейной, а население N – на логарифмической шкале.

Обратимся к тому, как за последние 4000 лет росла численность человечества (см. рис. 2). Эта картина развития человечества представлена на полулогарифмической сетке, когда население за 4000 лет возросло в 100 раз, что так озадачило демографов. Если бы население мира росло экспоненциально, то на такой сетке рост отображался бы прямой, чего ни в прошлом, ни в настоящем для человечества нет ни на одном этапе роста (см. рис. 3).

Рост человечества происходит совершенно иначе. На графике рис. 3 хорошо видно, как медленный вначале рост все ускоряется и по мере приближения к третьему тысячелетию вблизи рубежа веков население мира внезапно устремляется в бесконечность демографического взрыва, следуя графику гиперболы С.

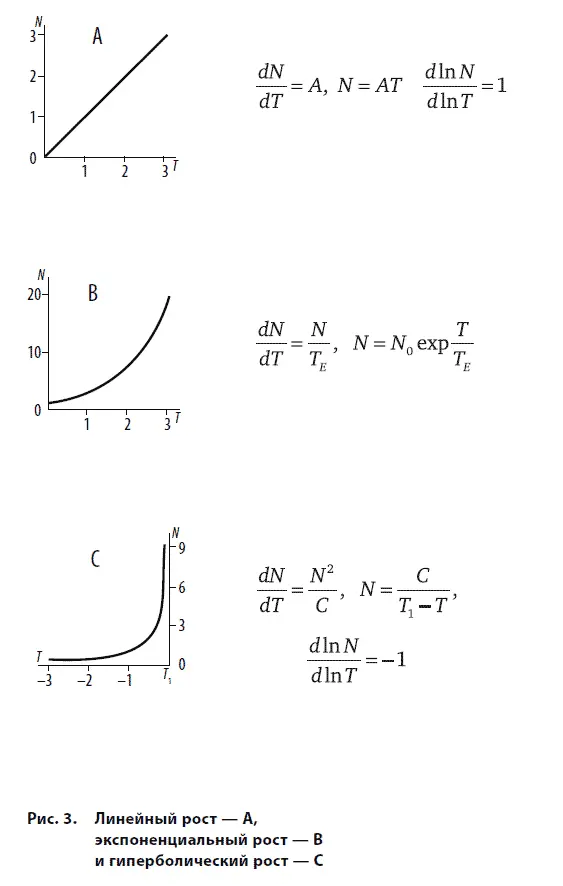
Эта закономерность роста, для которой также нет характерного времени роста, представляет для нас основной интерес, поскольку данные для населения мира за миллион лет с удивительной точностью описываются формулой:

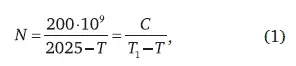
где С = 200 млрд – постоянная с размерностью [человек × годы], а время выражено в годах.

Следует отметить, что указанный закон роста очевидным образом возникает при первых попытках описать данные по росту человечества. Поэтому неудивительно, что к этой закономерности приходили в разное время многие исследователи. Одним из первых был английский эпидемиолог А. Маккендрик (1876–1943), на что автору указал крупнейший американский демограф Натан Кейфиц. Затем к этому выражению в 1960 г. обратились американский инженер Форстер и немецкий физик Хорнер.