Алексей Бочавер - Я познаю мир. Арктика и Антарктика

В основу существующей системы координатных линий положены две выделенные точки земного шара – его географические полюса. На земном шаре проводятся (мысленно, конечно) линии, проходящие от полюса до полюса по кратчайшему пути. Эти линии названы меридианами(от латинского Meridianus – полуденный), или линиями географической долготы.Название «меридиан» связано с тем, что в полдень тень, отбрасываемая предметом, вытянута строго в направлении с севера на юг (то есть по линии, проходящей от полюса до полюса). Меридиан можно провести через любую точку на поверхности планеты.

Далее, проводят (тоже мысленно) экватор(от латинского aequator – равный) – линию, равноудаленную от обоих полюсов. А параллельно ему – линии географической широты,или параллели(от греческого parallelos – «рядом идущий»). Так же, как меридиан, параллель можно провести через любую точку земной поверхности.

Теперь каждая точка на Земле может быть обозначена как перекресток параллели и меридиана. Дело за малым – придумать имена каждо 1: из координатных линий.

Справились с этой проблемой следующим образом. Окружность экватора разделили на 360 равных частей. Каждую часть назвали «градус», хотя эта единица не имеет ничего общего с градусами температуры. На самом деле этот градус –не расстояние, а угол, образованны^ двумя радиусами, отделяющими 1/360 часть окружности. Через каждую градусную точку – как и любую другую – можно провести меридиан.

Выбрав среди меридианов какой–нибудь один (безразлично, како^ именно), назовем его нулевым, или начальным. Ка почти всех современных картах (в том числе и российских) начальным считается меридиан, проходящий через обсерваторию в Гринвиче, вблизи Лондона. А до этого в России им был назначен меридиан, проходящий через Пулковскую обсерваторию, вблизи Санкт–Петербурга.

И в обе стороны от нулевого будем отсчитывать меридианы, обозначая их номером градуса и указывая направление счета (к востоку или к западу от начального меридиана).

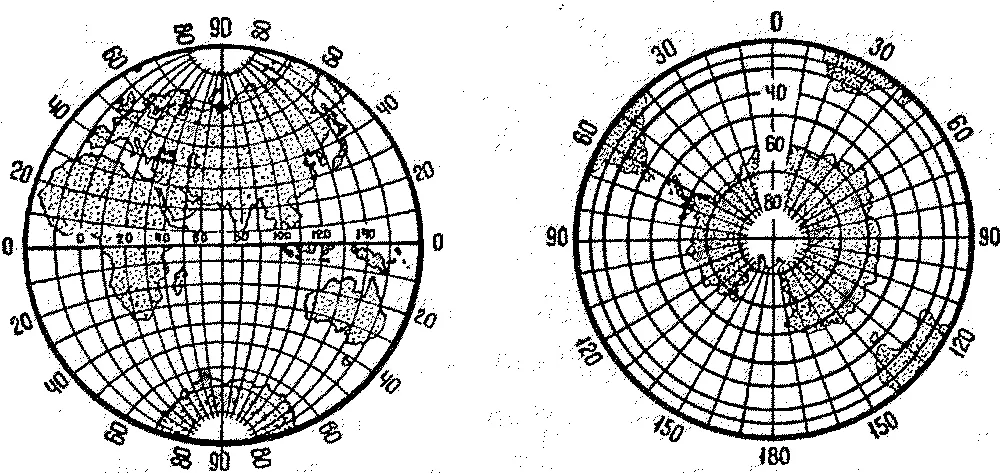
Карта меридианов и параллелей

Обойдя (в любом направлении) пол–Земли, мы доберемся до меридиана 180–го градуса. А остальные меридианы, проходящие через градусные точки, будут обозначаться, например, как меридиан 37–го градуса к востоку от гринвичского. Чтобы запись была короче, слово «градус» заменили значком (°) – опять–таки, как у температуры. И имя того же меридиана мозкет быть записано так: 37° в.д. (восточной долготы).

Но градусных точек всего 360, и легко сосчитать, что при длине экватора около 40.000 км расстояние между соседними такими точками составит (на акваторе) больше 100 километров. Не особенно точен такой адрес! Чтобы уточнить его, каждый градус поделили на шестьдесят частей, назвав каждую минутой(без всякой связи со временем, разве что каждый градус делится на 60 частей подобно часу) и обозначив штрихом (').

К примеру, более точное обозначение географической долготы центра Москвы выглядит так: 37°12'в.д. Если же нужна еще более высокая точность, пользуются тем же приемом, разбивая каждую минуту на 60 частей, называемых секундамии обозначаемых двойным штрихом ("). Запись такая: 37 12’10"в.д. На практике секундами пользуются редко.

С параллелями поступают сходным образом. Экватор назначен «нулевой параллелью», а остальные обозначают с помощью градусов, минут и секунд – опять–таки в две стороны, к югу и к северу от экватора. Например, географическая широта центра Москвы 55 45' с.ш. (северной широты).

Таким образом, полный адрес точки на земной поверхности состоит из четырех частей. Например, 37°12' в.д., 55°45' с.ш. (Красная площадь в Москве).

Вероятно, это не самая простая из возможных систем. Например, артиллеристы в сходной ситуации поделили окружность не на 360, а затем еще на 60, а сразу на 1000 частей, и называют их тысячные.

Но та система, которую мы описали, принята во всем мире, и пользуются ею много лет. Так что и в будущем она, видимо, сохранится.

А географические координаты географических полюсов Земли записываются проще, чем у других точек. 90° северной или южной широты – и мы имеем дело с Северным или Южным полюсом. Долготу при этом не обозначают: ведь на полюсах сходятся все меридианы.