БСЭ БСЭ - Большая Советская Энциклопедия (АЭ)

Величины f и а — наиболее важные характеристики А. р. г. В общем случае а и f зависят от скорости движения потока газа, материала и температуры стенки, от гладкости её поверхности, наличия на поверхности адсорбированных молекул газа и т. д. Однако точных зависимостей a и f от определяющих их параметров ещё не получено.

Эксперименты, проведённые в широком диапазоне скоростей для различных газов и материалов, дают значения a в широких пределах — от 0,95 до 0,02. Установлено, что уменьшение a происходит при увеличении скорости молекул газа и отношения молекулярных масс m 1 и m 2 тела и газа. Так например, если вместо тела из алюминия взять тело из свинца, то коэффициент аккомодации уменьшается примерно в 4 раза, что приводит к уменьшению аэродинамического нагрева. Коэффициент f изменяется меньше: от 0,98 до 0,7.

Разреженность среды проявляется в совершенно необычном поведении аэродинамических коэффициентов. Так, коэффициент сопротивления сферы C x зависит от отношения абсолютной температуры тела T w к абсолютной температуре потока T iа также от a и f ( рис. 2 ), в то время как в сплошной среде таких зависимостей не наблюдается. Коэффициенты, характеризующие теплообмен, также отличаются качественно и количественно от континуальных.

Промежуточная область. При l/d ~ 1 существенна роль межмолекулярных столкновений, когда отражённые от поверхности тела молекулы значительно искажают распределение скоростей молекул набегающего потока. Теоретические решения для свободномолекулярного потока здесь неприемлемы. Вместе с тем, такое течение ещё нельзя рассматривать как течение сплошной среды. Промежуточная область весьма трудна для математического анализа.

Течение со скольжением. Если размер тела d в десятки раз больше l , т. е. l/d < 1, то в потоке уже могут возникать характерные для газовой динамики ударные волны и пограничные слои на поверхности тел. Однако, в отличие от обычного пограничного слоя, температура примыкающего к стенке газа T a не равна температуре стенки T w, а скорость потока на поверхности тела не равна нулю (поток проскальзывает). Скачок температуры ( T w — T a ) пропорционален l и зависит от f . Скорость скольжения также пропорциональна l и зависит от f . Эксперименты показывают, что при увеличении разреженности газа происходит утолщение ударной волны, возрастает и толщина пограничного слоя, но значительно медленнее ( рис. 3 ). Ударная волна может распространиться на всю область сжатого газа в районе передней критической точки обтекаемого тела и слиться с пограничным слоем. Распределение плотности в районе передней критической точки становится плавным, а не скачкообразным, как в континууме. При расчёте течений со скольжением поток описывается обычными уравнениями газовой динамики, но с граничными условиями, учитывающими скачок температуры и скорость скольжения.

Границы упомянутых областей течения весьма условны. Для различных тел появление признаков, характеризующих ту или иную область, может наступить при разных значениях параметра разреженности l/d. В связи со сложностью теоретических расчётов и необходимостью определения ряда эмпирических констант, входящих в практические методы расчёта тепловых и аэродинамических характеристик, особое значение в А. р. г. приобретает эксперимент.

Лит.: Аэродинамика разреженных газов, сб. 1, под ред. С. В. Валландера, Л., 1963; Паттерсон Г. Н., Молекулярное течение газов, пер. с англ., М., 1960; Тзян Х. Ш., Аэродинамика разреженных газов, в сборнике: Газовая динамика, сб. статей, пер. с англ., под ред. С. Г. Попова и С. В. фальковича, М., 1950.

Л. В. Козлов.

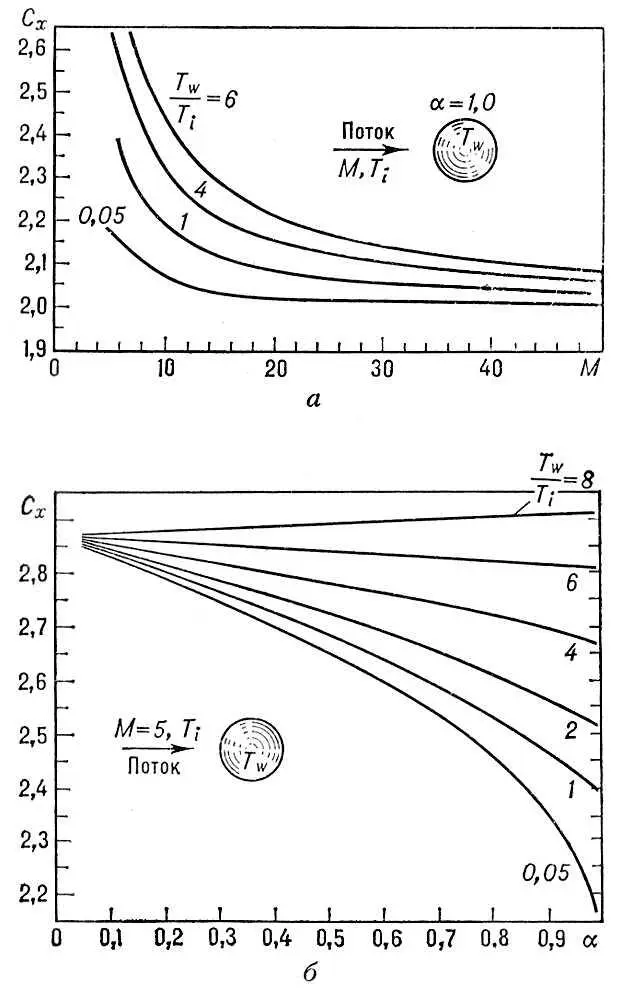
Рис. 2. Зависимость коэффициента сопротивления сферы C x в свободномолекулярном потоке при различных отношениях абсолютной температуры тела T w к абсолютной температуре потока T i : а — от числа М полёта для a = 1,0 и б — от коэффициента аккомодации a .

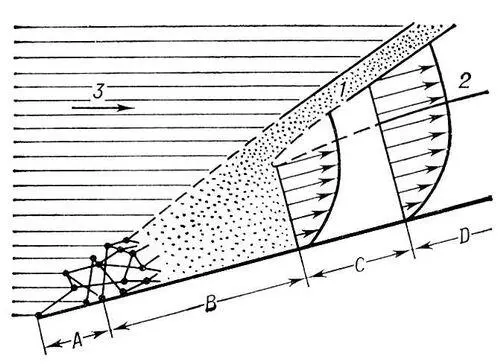
Рис. 1. Условная схема различных течений около плоской длинной бесконечно тонкой пластины, обтекаемой сверхзвуковым потоком: А — свободномолекулярное течение с однократными соударениями; В — промежуточная область с многократными соударениями; С — течение со скольжением; D — континуум; 1 — ударная волна; 2 — граница пограничного слоя (стрелки показывают значения скорости на данном расстоянии от стенки; 3 — макроскопическое движение молекул. (Масштабы зон и областей не соблюдены.)