Очамчи'ра,город (с 1926), центр Очамчирского района Абхазской АССР. Расположен на берегу Чёрного моря, в устье р. Галидзга. Ж.-д. станция на линии Армавир — Самтредиа; от О.— ветка (26 км 2 ) на Ткварчели. 19 тыс. жителей (1974). Маслоэкстракционный, консервный заводы, 2 чайные фабрики, табачно-ферментационное предприятие, промкомбинат. Строится (1974) птицефабрика.
В районе О. открыты разновременные археологические памятники. Наиболее полно исследовано (М. М. Иващенко и Л. Н. Соловьев, 1935—36) поселение в 5 км к С. от О., содержавшее слои эпохи ранней бронзы, античного времени и средневековья. В древнейшем слое, относящемся к 3-му тыс. до н. э., найдены обломки главным образом груболепных глиняных сосудов разных форм, грузила и др. орудия из гальки, каменные зернотёрки, кремнёвые наконечники стрел, вкладыши к серпам и различные костяные орудия. Инвентарь этого слоя близок к находкам из дольменов и др. памятников эпохи ранней бронзы Абхазии и Колхидской низменности. В районе О. известны также поселения с так называемой текстильной керамикой, относящиеся к 1-му тыс. до н. э. Предполагается, что в античное время здесь была греческая фактория.
Лит.: Соловьев Л. Н., Энеолитическое селище у Очемчирского порта в Абхазии, в кн.: Материалы по истории Абхазии, сб. 1, Сухуми, 1939; Анчабадзе З. В., История и культура древней Абхазии, М., 1964.
Оча'нка(Euphrasia), род растений семейства норичниковых. Однолетние, редко многолетние полупаразитные травы с супротивными, сидячими, пильчатыми или надрезанно-зубчатыми листьями. Цветки с двугубым венчиком, мелкие, большей частью белые, лиловые или пурпуровые, сидят по одному в пазухах прицветных листьев и образуют длинные колосовидные соцветия. Плод — коробочка. Около 200 большей частью полиморфных видов, произрастающих в Северном полушарии, а также в горах Малайского архипелага, в Австралии и умеренном поясе Южной Америки. В СССР — около 60 видов, растут почти повсеместно по лугам, выгонам, полянам, кустарникам. Наиболее распространена О. прямая (Е. stricta), паразитирующая, как и многие др. виды О., преимущественно на корнях злаков (иногда значительно снижает урожайность лугов).
Лит.: флора СССР, т. 22, М.— Л., 1955.
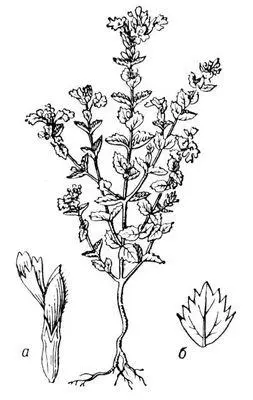
Очанка прямая; а — цветок, б — лист.
Очёр,город, центр Очёрского района Пермской области РСФСР. Расположен на р. Очёр (приток Камы). Конечный пункт ветки (23 км ) от ж.-д. станции Верещагино (на линии Киров — Пермь). 15,4 тыс. жителей (1974). Заводы: машиностроительный (выпускает трубоукладчики) и механический. Индустриально-педагогический техникум.
Очереде'й тео'рия,раздел массового обслуживания теории . О. т. изучает системы, в которых требования, застающие систему занятой, не теряются, а ожидают её освобождения и затем обслуживаются в том или ином порядке (часто с предоставлением приоритета определённым категориям требований). Выводы О. т. используют для рационального планирования систем массового обслуживания. С математической точки зрения задачи О. т. могут быть включены в теорию случайных процессов , а ответы часто бывают выражены в терминах Лапласа преобразований искомых характеристик. Применение методов О. т. необходимо даже в простейших случаях для правильного понимания статистических закономерностей, возникающих в системах массового обслуживания.
Пример. Пусть имеется один обслуживающий прибор, на который поступает случайный поток требований. Если в момент поступления требования прибор свободен, то оно сразу начинает обслуживаться. В противном случае оно становится в очередь и прибор обслуживает требования одно за другим в порядке их поступления. Пусть а — среднее число требований, поступающих за время одного обслуживания, а < 1 и Т — длительность периода занятости, то есть промежутка времени от момента занятия прибора каким-либо требованием, заставшим прибор свободным, до первого момента полного освобождения прибора. О. т. показывает, что при естественных допущениях математическое ожидание Т равно m = 1/(1 — а), а дисперсия равна (1 + a ) m 3 (так, при а = 0,8 соответствующие значения равны 5 и 225). Таким образом, для «хорошо загруженного» обслуживающего прибора (то есть при а, близких к 1) среднее значение m случайной величины Т является весьма ненадёжной характеристикой Т.
Читать дальше

