d 1= x 1— a,…, d n= x n— a
называются истинными ошибками. В терминах вероятностной О. т. все d i трактуются как случайные величины; независимость измерений понимается как взаимная независимость случайных величин d 1 ,..., d n . Равноточность измерений в широком смысле истолковывается как одинаковая распределённость: истинные ошибки равноточных измерений суть одинаково распределённые случайные величины. При этом математическое ожидание случайных ошибок b = Ed 1 =.. .= Еd n называется систематической ошибкой, а разности d 1 — b,..., d n — b — случайными ошибками. Таким образом, отсутствие систематической ошибки означает, что b = 0 , и в этой ситуации d 1 ,..., d n суть случайные ошибки. Величину 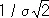 , где а — квадратичное отклонение , называют мерой точности (при наличии систематической ошибки мера точности выражается отношением
, где а — квадратичное отклонение , называют мерой точности (при наличии систематической ошибки мера точности выражается отношением 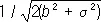 . Равноточность измерений в узком смысле понимается как одинаковость меры точности всех результатов измерений. Наличие грубых ошибок означает нарушение равноточности (как в широком, так и в узком смысле) для некоторых отдельных измерений. В качестве оценки неизвестной величины а обычно берут арифметическое среднее из результатов измерений
. Равноточность измерений в узком смысле понимается как одинаковость меры точности всех результатов измерений. Наличие грубых ошибок означает нарушение равноточности (как в широком, так и в узком смысле) для некоторых отдельных измерений. В качестве оценки неизвестной величины а обычно берут арифметическое среднее из результатов измерений
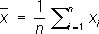 ,
,
а разности D 1= x 1 — 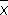 ,..., D n= x n—
,..., D n= x n— 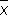 называются кажущимися ошибками. Выбор
называются кажущимися ошибками. Выбор 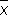 в качестве оценки для а основан на том, что при достаточно большом числе n равноточных измерений, лишённых систематической ошибки, оценка
в качестве оценки для а основан на том, что при достаточно большом числе n равноточных измерений, лишённых систематической ошибки, оценка 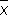 с вероятностью, сколь угодно близкой к единице, сколь угодно мало отличается от неизвестной величины а (см. Больших чисел закон ); оценка
с вероятностью, сколь угодно близкой к единице, сколь угодно мало отличается от неизвестной величины а (см. Больших чисел закон ); оценка 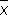 лишена систематической ошибки (оценки с таким свойством называются несмещенными); дисперсия оценки есть
лишена систематической ошибки (оценки с таким свойством называются несмещенными); дисперсия оценки есть
D 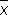 = E (
= E ( 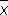 — а ) 2 = s 2/n.
— а ) 2 = s 2/n.
Опыт показывает, что практически очень часто случайные ошибки d i подчиняются распределениям, близким к нормальному (причины этого вскрыты так называемыми предельными теоремами теории вероятностей). В этом случае величина 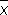 имеет мало отличающееся от нормального распределение, с математическим ожиданием а и дисперсией s 2 /n. Если распределения d i в точности нормальны, то дисперсия всякой другой несмещенной оценки для а, например медианы , не меньше D
имеет мало отличающееся от нормального распределение, с математическим ожиданием а и дисперсией s 2 /n. Если распределения d i в точности нормальны, то дисперсия всякой другой несмещенной оценки для а, например медианы , не меньше D 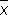 . Если же распределение d i отлично от нормального, то последнее свойство может не иметь места.
. Если же распределение d i отлично от нормального, то последнее свойство может не иметь места.
Если дисперсия s 2 отдельных измерений заранее известна, то для её оценки пользуются величиной
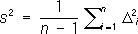
(E s 2= s 2, т. е. s 2— несмещенная оценка для s 2 ), если случайные ошибки d i имеют нормальное распределение, то отношение
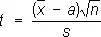
подчиняется Стьюдента распределению с n — 1 степенями свободы. Этим можно воспользоваться для оценки погрешности приближённого равенства а » 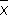 (см. Наименьших квадратов метод ).
(см. Наименьших квадратов метод ).
Величина ( n — 1 ) s 2/ s 2 при тех же предположениях имеет распределение c 2(см. «Хи-квадрат» распределение ) с n — 1 степенями свободы. Это позволяет оценить погрешность приближённого равенства s » s. Можно показать, что относительная погрешность | s — s | Is не будет превышать числа q с вероятностью
w = F ( z 2, n — 1 ) — F ( z 1, n — 1 ) ,
где F ( z, n — 1 ) — функция распределения c 2,
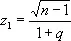 ,
, 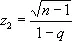 .
.
Читать дальше

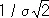 , где а — квадратичное отклонение , называют мерой точности (при наличии систематической ошибки мера точности выражается отношением
, где а — квадратичное отклонение , называют мерой точности (при наличии систематической ошибки мера точности выражается отношением 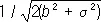 . Равноточность измерений в узком смысле понимается как одинаковость меры точности всех результатов измерений. Наличие грубых ошибок означает нарушение равноточности (как в широком, так и в узком смысле) для некоторых отдельных измерений. В качестве оценки неизвестной величины а обычно берут арифметическое среднее из результатов измерений
. Равноточность измерений в узком смысле понимается как одинаковость меры точности всех результатов измерений. Наличие грубых ошибок означает нарушение равноточности (как в широком, так и в узком смысле) для некоторых отдельных измерений. В качестве оценки неизвестной величины а обычно берут арифметическое среднее из результатов измерений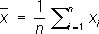 ,
,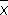 ,..., D n= x n—
,..., D n= x n— 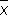 называются кажущимися ошибками. Выбор
называются кажущимися ошибками. Выбор 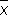 в качестве оценки для а основан на том, что при достаточно большом числе n равноточных измерений, лишённых систематической ошибки, оценка
в качестве оценки для а основан на том, что при достаточно большом числе n равноточных измерений, лишённых систематической ошибки, оценка 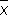 с вероятностью, сколь угодно близкой к единице, сколь угодно мало отличается от неизвестной величины а (см. Больших чисел закон ); оценка
с вероятностью, сколь угодно близкой к единице, сколь угодно мало отличается от неизвестной величины а (см. Больших чисел закон ); оценка 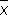 лишена систематической ошибки (оценки с таким свойством называются несмещенными); дисперсия оценки есть
лишена систематической ошибки (оценки с таким свойством называются несмещенными); дисперсия оценки есть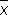 = E (
= E ( 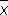 — а ) 2 = s 2/n.
— а ) 2 = s 2/n.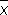 имеет мало отличающееся от нормального распределение, с математическим ожиданием а и дисперсией s 2 /n. Если распределения d i в точности нормальны, то дисперсия всякой другой несмещенной оценки для а, например медианы , не меньше D
имеет мало отличающееся от нормального распределение, с математическим ожиданием а и дисперсией s 2 /n. Если распределения d i в точности нормальны, то дисперсия всякой другой несмещенной оценки для а, например медианы , не меньше D 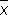 . Если же распределение d i отлично от нормального, то последнее свойство может не иметь места.
. Если же распределение d i отлично от нормального, то последнее свойство может не иметь места.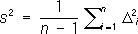
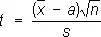
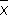 (см. Наименьших квадратов метод ).
(см. Наименьших квадратов метод ).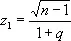 ,
, 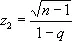 .
.