Лит.: Общая селекция и семеноводство полевых культур, 3 изд., М., 1958; Пустовойт В. С., Избр. труды М., 1966; Гуляев Г. В., Гужов Ю. Л., Селекция и семеноводство полевых культур, М., 1972.
Г. В. Гуляев.
Отбо'ра пра'вила,правила, определяющие возможные квантовые переходы для атомов, молекул, атомных ядер, взаимодействующих элементарных частиц и др. О. п. устанавливают, какие квантовые переходы разрешены (вероятность перехода велика) и какие запрещены — строго (вероятность перехода равна нулю) или приближённо (вероятность перехода мала); соответственно О. п. разделяют на строгие и приближённые. При характеристике состояний системы с помощью квантовых чисел О. п. определяют возможные изменения этих чисел при переходе рассматриваемого типа.
О. п. связаны с симметрией квантовых систем, т. е. с неизменностью (инвариантностью) их свойств при определённых преобразованиях, в частности координат и времени, и с соответствующими сохранения законами . Переходы с нарушением строгих законов сохранения (например, энергии, импульса, момента количества движения, электрического заряда и т.д. замкнутой системы) абсолютно исключаются.
Для излучателей квантовых переходов между стационарными состояниями атомов и молекул очень важны строгие О. п. для квантовых чисел J и m j , определяющих возможные значения полного момента количества движения М и его проекции M z по правилам квантования: 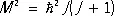 ,
, 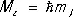 (
( 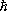 — Планка постоянная , J и m J — целые или полуцелые числа, причём m J = J , J — 1,......, — J ; см. Квантовые числа ). Эти правила связаны с равноправием в пространстве всех направлений (для любой точки — сферическая симметрия) и всех направлений, перпендикулярных выделенной оси z (аксиальная симметрия), и соответствуют сохранению момента количества движения и его проекции на ось z . Из законов сохранения полного момента количества движения и его проекции для системы, состоящей из микрочастиц и из испускаемых, поглощаемых и рассеиваемых фотонов, следует, что при квантовом переходе J и m J могут изменяться в случае электрического и магнитного дипольных излучений (см. Излучение электромагнитное) лишь на 0, ±1, а в случае электрического квадрупольного излучения (а также в случае комбинационного рассеяния света ) — на 0, ±1, ±2.
— Планка постоянная , J и m J — целые или полуцелые числа, причём m J = J , J — 1,......, — J ; см. Квантовые числа ). Эти правила связаны с равноправием в пространстве всех направлений (для любой точки — сферическая симметрия) и всех направлений, перпендикулярных выделенной оси z (аксиальная симметрия), и соответствуют сохранению момента количества движения и его проекции на ось z . Из законов сохранения полного момента количества движения и его проекции для системы, состоящей из микрочастиц и из испускаемых, поглощаемых и рассеиваемых фотонов, следует, что при квантовом переходе J и m J могут изменяться в случае электрического и магнитного дипольных излучений (см. Излучение электромагнитное) лишь на 0, ±1, а в случае электрического квадрупольного излучения (а также в случае комбинационного рассеяния света ) — на 0, ±1, ±2.
Другое важное О. п. связано с законом сохранения полной чётности для изолированной квантовой системы (этот закон нарушается лишь слабым взаимодействием элементарных частиц). Квантовые состояния атомов, всегда имеющих центр симметрии, а также тех молекул и кристаллов, которые имеют такой центр, делятся на чётные и нечётные по отношению к пространств. инверсии (отражению в центре симметрии, т. е. к преобразованию координат х' ® — х , у' ® — у , z' ® — z ); в этих случаях справедлив т. н. альтернативный запрет для излучательных квантовых переходов: для электрического дипольного излучения запрещены переходы между состояниями одинаковой чётности (т. е. между чётными или между нечётными состояниями), а для дипольного магнитного и квадрупольного электрического излучений (и для комбинационного рассеяния) запрещены переходы между состояниями различной чётности (т. е. между чётными и нечётными состояниями. В силу этого запрета можно наблюдать, частности в атомных спектрах астрономических объектов, линии, соответствующие магнитным дипольным и электрическим квадрупольным переходам, обладающим очень малой вероятностью по сравнению с дипольными электрическими переходами (т. н. запрещённые линии ).
Наряду с точными О. п. по J и m J существенны приближённые О. п. при дипольном излучении атомов для квантовых чисел, определяющих величины орбитальных и спиновых моментов электронов и проекций этих моментов. Например, для атома с одним внешним электроном азимутальное квантовое число l , определяющее величину орбитального момента электрона M lM 2 l = 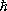 2 l ( l + 1), может изменяться на ± 1 (D l = 0 невозможно, т.к. состояния с одинаковыми l имеют одинаковую чётность: они чётные при чётном l и нечётные при нечётном l ). Для сложных атомов квантовое число L , определяющее полный орбитальный момент всех электронов, подчинено приближённому О. п. D L = 0, ±1, а квантовое число S , определяющее полный спиновый момент всех электронов (и мультиплетность k = 2 S + 1), — приближённому О. п. D S = 0, справедливому, если не учитывать спин-орбитальное взаимодействие . Учёт этого взаимодействия нарушает последнее О. п., и появляются т. н. интеркомбинационные переходы, вероятности которых тем больше, чем больше атомный номер элемента.
2 l ( l + 1), может изменяться на ± 1 (D l = 0 невозможно, т.к. состояния с одинаковыми l имеют одинаковую чётность: они чётные при чётном l и нечётные при нечётном l ). Для сложных атомов квантовое число L , определяющее полный орбитальный момент всех электронов, подчинено приближённому О. п. D L = 0, ±1, а квантовое число S , определяющее полный спиновый момент всех электронов (и мультиплетность k = 2 S + 1), — приближённому О. п. D S = 0, справедливому, если не учитывать спин-орбитальное взаимодействие . Учёт этого взаимодействия нарушает последнее О. п., и появляются т. н. интеркомбинационные переходы, вероятности которых тем больше, чем больше атомный номер элемента.
Читать дальше

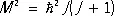 ,
, 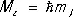 (
( 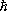 — Планка постоянная , J и m J — целые или полуцелые числа, причём m J = J , J — 1,......, — J ; см. Квантовые числа ). Эти правила связаны с равноправием в пространстве всех направлений (для любой точки — сферическая симметрия) и всех направлений, перпендикулярных выделенной оси z (аксиальная симметрия), и соответствуют сохранению момента количества движения и его проекции на ось z . Из законов сохранения полного момента количества движения и его проекции для системы, состоящей из микрочастиц и из испускаемых, поглощаемых и рассеиваемых фотонов, следует, что при квантовом переходе J и m J могут изменяться в случае электрического и магнитного дипольных излучений (см. Излучение электромагнитное) лишь на 0, ±1, а в случае электрического квадрупольного излучения (а также в случае комбинационного рассеяния света ) — на 0, ±1, ±2.
— Планка постоянная , J и m J — целые или полуцелые числа, причём m J = J , J — 1,......, — J ; см. Квантовые числа ). Эти правила связаны с равноправием в пространстве всех направлений (для любой точки — сферическая симметрия) и всех направлений, перпендикулярных выделенной оси z (аксиальная симметрия), и соответствуют сохранению момента количества движения и его проекции на ось z . Из законов сохранения полного момента количества движения и его проекции для системы, состоящей из микрочастиц и из испускаемых, поглощаемых и рассеиваемых фотонов, следует, что при квантовом переходе J и m J могут изменяться в случае электрического и магнитного дипольных излучений (см. Излучение электромагнитное) лишь на 0, ±1, а в случае электрического квадрупольного излучения (а также в случае комбинационного рассеяния света ) — на 0, ±1, ±2.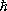 2 l ( l + 1), может изменяться на ± 1 (D l = 0 невозможно, т.к. состояния с одинаковыми l имеют одинаковую чётность: они чётные при чётном l и нечётные при нечётном l ). Для сложных атомов квантовое число L , определяющее полный орбитальный момент всех электронов, подчинено приближённому О. п. D L = 0, ±1, а квантовое число S , определяющее полный спиновый момент всех электронов (и мультиплетность k = 2 S + 1), — приближённому О. п. D S = 0, справедливому, если не учитывать спин-орбитальное взаимодействие . Учёт этого взаимодействия нарушает последнее О. п., и появляются т. н. интеркомбинационные переходы, вероятности которых тем больше, чем больше атомный номер элемента.
2 l ( l + 1), может изменяться на ± 1 (D l = 0 невозможно, т.к. состояния с одинаковыми l имеют одинаковую чётность: они чётные при чётном l и нечётные при нечётном l ). Для сложных атомов квантовое число L , определяющее полный орбитальный момент всех электронов, подчинено приближённому О. п. D L = 0, ±1, а квантовое число S , определяющее полный спиновый момент всех электронов (и мультиплетность k = 2 S + 1), — приближённому О. п. D S = 0, справедливому, если не учитывать спин-орбитальное взаимодействие . Учёт этого взаимодействия нарушает последнее О. п., и появляются т. н. интеркомбинационные переходы, вероятности которых тем больше, чем больше атомный номер элемента.