ds 2 = ( cdt ) 2 - dx 2 - dy 2 - dz 2(7)
где t — время, х, у, z — прямоугольные декартовы (пространственные) координаты. Эта система координат называется галилеевой. Выражение (7) имеет вид, аналогичный выражению для квадрата расстояния в евклидовом трёхмерном пространстве в декартовых координатах (с точностью до числа измерений и знаков перед квадратами дифференциалов в правой части). Такое пространство-время называют плоским, евклидовым, или, точнее, псевдоевклидовым, подчёркивая особый характер времени: в выражении (7) перед ( cdt ) 2стоит знак «+», в отличие от знаков «—» перед квадратами дифференциалов пространственных координат. Таким образом, специальная теория относительности является теорией физических процессов в плоском пространстве-времени (пространстве-времени Минковского; см. Минковского пространство ).
В пространстве-времени Минковского не обязательно пользоваться декартовыми координатами, в которых интервал записывается в виде (7). Можно ввести любые криволинейные координаты. Тогда квадрат интервала ds 2будет выражаться через эти новые координаты общей квадратичной формой:
ds 2= g ik dx i dx k(8)
( i , k = 0, 1, 2, 3), где x 1 , x 2 , x 3 — произвольные пространств, координаты, x 0 = ct — временная координата (здесь и далее по дважды встречающимся индексам производится суммирование). С физической точки зрения переход к произвольным координатам означает и переход от инерциальной системы отсчёта к системе, вообще говоря, движущейся с ускорением (причём в общем случае разным в разных точках), деформирующейся и вращающейся, и использование в этой системе не декартовых пространственных координат. Несмотря на кажущуюся сложность использования таких систем, практически они иногда оказываются удобными. Но в специальной теории относительности всегда можно пользоваться и галилеевой системой, в которой интервал записывается особенно просто. [В этом случае в формуле (8) g ik = 0 при i ¹ k, g 00 = 1, g ii = —1 при i = 1, 2, 3.]
В общей теории относительности пространство-время не плоское, а искривленное. В искривленном пространстве-времени (в конечных, не малых, областях) уже нельзя ввести декартовы координаты, и использование криволинейных координат становится неизбежным. В конечных областях такого искривленного пространства-времени ds 2записывается в криволинейных координатах в общем виде (8). Зная g ikкак функции четырёх координат, можно определить все геометрические свойства пространства-времени. Говорят, что величины g ikопределяют метрику пространства-времени , а совокупность всех g ikназывают метрическим тензором. С помощью g ikвычисляются темп течения времени в разных точках системы отсчёта и расстояния между точками в трёхмерном пространстве. Так, формула для вычисления бесконечно малого интервала времени d t по часам, покоящимся в системе отсчёта, имеет вид:
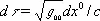
При наличии поля Т. величина g 00в разных точках разная, следовательно, темп течения времени зависит от поля Т. Оказывается, что чем сильнее поле, тем медленнее течёт время по сравнению с течением времени для наблюдателя вне поля.
Математическим аппаратом, изучающим неевклидову геометрию (см. Риманова геометрия ) в произвольных координатах, является тензорное исчисление . Общая теория относительности использует аппарат тензорного исчисления, её законы записываются в произвольных криволинейных координатах (это означает, в частности, запись в произвольных системах отсчёта), как говорят, в ковариантном виде.
Основная задача теории Т.— определение гравитационного поля, что соответствует в теории Эйнштейна нахождению геометрии пространства-времени. Эта последняя задача сводится к нахождению метрического тензора g ik .
Уравнения тяготения Эйнштейна связывают величины g ikс величинами, характеризующими материю, создающую поле: плотностью, потоками импульса и т.п. Эти уравнения записываются в виде:
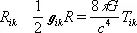 . (9)
. (9)
Здесь R ik — так называемый тензор Риччи, выражающийся через g ik, его первые и вторые производные по координатам; R = R ik g ik(величины g ik определяются из уравнений g ik g km = 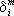 , где
, где 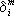 — Кронекера символ ); T ik — так называемый тензор энергии-импульса материи, компоненты которого выражаются через плотность, потоки импульса и др. величины, характеризующие материю и её движение (под физической материей подразумеваются обычное вещество, электромагнитное поле, все др. физические поля).
— Кронекера символ ); T ik — так называемый тензор энергии-импульса материи, компоненты которого выражаются через плотность, потоки импульса и др. величины, характеризующие материю и её движение (под физической материей подразумеваются обычное вещество, электромагнитное поле, все др. физические поля).
Читать дальше

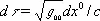
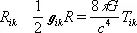 . (9)
. (9)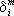 , где
, где 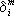 — Кронекера символ ); T ik — так называемый тензор энергии-импульса материи, компоненты которого выражаются через плотность, потоки импульса и др. величины, характеризующие материю и её движение (под физической материей подразумеваются обычное вещество, электромагнитное поле, все др. физические поля).
— Кронекера символ ); T ik — так называемый тензор энергии-импульса материи, компоненты которого выражаются через плотность, потоки импульса и др. величины, характеризующие материю и её движение (под физической материей подразумеваются обычное вещество, электромагнитное поле, все др. физические поля).