Лит.: Струве В. В., Новые данные об организации труда и социальной структуре общества Сумера эпохи III династии Ура, «Советское востоковедение», 1949, № 6; Тюменев А. И., Государственное хозяйство древнего Шумера, М. – Л., 1956.
Умм-Саи'д,город и порт в Катаре, на побережье Персидского зал. Около 2 тыс. жителей Конечный пункт шоссе, пересекающего полуостров Катар с З. на В. Близ У.-С. – нефтеочистительный завод (нефть поступает по трубопроводу с месторождения в районе Духана).
Умм-эр-Рби'я,река на З. Марокко. Длина 556 км. Берёт начало в горах Среднего Атласа, впадает в Атлантический океан. В горах – бурный поток, по выходе из гор – спокойная равнинная река. Главные притоки – Эль-Абид и Тесаут. Бурные паводки весной (таяние снегов в горах), после дождей зимой (средний расход воды в это время около 200 м 3 /сек ) , в сухой сезон летом – сильно обмелевает. На У.-э.-Р. и притоке Эль-Абид – ГЭС. Воды У.-э.-Р. широко используются для орошения.
Умноже'ние,операция образования по двум данным объектам а и b, называемым сомножителями, третьего объекта с, называемого произведением. У. обозначается знаком Х (ввёл англ. математик У. Оутред в 1631) или • (ввёл нем. учёный Г. Лейбниц в 1698); в буквенном обозначении эти знаки опускаются и вместо а ´ b или а • b пишут ab. У. имеет различный конкретный смысл и соответственно различные конкретные определения в зависимости от конкретного вида сомножителей и произведения. У. целых положительных чисел есть, по определению, действие, относящее числам а и b третье число с, равное сумме b слагаемых, каждое из которых равно а, так что ab = а + а +... + а ( b слагаемых). Число а называется множимым, b – множителем. У. дробных чисел  и
и  определяется равенством
определяется равенством 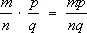 (см. Дробь ) . У. рациональных чисел даёт число, абсолютная величина которого равна произведению абсолютных величин сомножителей, имеющее знак плюс (+), если оба сомножителя одинакового знака, и знак минус (–), если они разного знака. У. иррациональных чисел определяется при помощи У. их рациональных приближений. У. комплексных чисел, заданных в форме a = а + bi и b = с + di, определяется равенством ab = ac – bd + ( ad + bc ) i. При У. комплексных чисел, записанных в тригонометрической форме:
(см. Дробь ) . У. рациональных чисел даёт число, абсолютная величина которого равна произведению абсолютных величин сомножителей, имеющее знак плюс (+), если оба сомножителя одинакового знака, и знак минус (–), если они разного знака. У. иррациональных чисел определяется при помощи У. их рациональных приближений. У. комплексных чисел, заданных в форме a = а + bi и b = с + di, определяется равенством ab = ac – bd + ( ad + bc ) i. При У. комплексных чисел, записанных в тригонометрической форме:
a = r 1(cosj 1+ i sin j 1),
b = r 2(cosj 2+ i sin j 2),
их модули перемножаются, а аргументы складываются:
ab = r 1 r 2{cos (j 1+ j 2) + i sin ((j 1+ j 2)}.
У. чисел однозначно и обладает следующими свойствами:
1) ab = ba (коммутативность, переместительный закон);
2) a ( bc ) = ( ab ) c (ассоциативность, сочетательный закон);
3) a ( b + c ) = ab + ac (дистрибутивность, распределительный закон). При этом всегда а ×0 = 0; a× 1 = а. Указанные свойства лежат в основе обычной техники У. многозначных чисел.
Дальнейшее обобщение понятия У. связано с возможностью рассматривать числа как операторы в совокупности векторов на плоскости. Например, комплексному числу r (cosj + i sin j) соответствует оператор растяжения всех векторов в r раз и поворота их на угол j вокруг начала координат. При этом У. комплексных чисел отвечает У. соответствующих операторов, т. е. результатом У. будет оператор, получающийся последовательным применением двух данных операторов. Такое определение У. операторов переносится и на другие виды операторов, которые уже нельзя выразить при помощи чисел (например, линейные преобразования). Это приводит к операциям У. матриц, кватернионов, рассматриваемых как операторы поворота и растяжения в трёхмерном пространстве, ядер интегральных операторов и т.д. При таких обобщениях могут оказаться невыполненными некоторые из перечисленных выше свойств У., чаще всего – свойство коммутативности (некоммутативная алгебра). Изучение общих свойств операции У. входит в задачи общей алгебры, в частности теории групп и колец.
Умножи'тель частоты',электронное (реже электромагнитное) устройство, предназначенное для увеличения в целое число раз частоты подводимых к нему периодических электрических колебаний. Отношение f вых/ f вх( f вхи f вых– частоты колебаний соответственно на входе и выходе У. ч.) называется коэффициента умножения частоты m ( m ³ 2 ; может достигать нескольких десятков). Характерная особенность У. ч. – постоянство т при изменении (в некоторой конечной области) f вх , а также параметров У. ч. (например, резонансных частот колебательных контуров или резонаторов, входящих в состав У. ч.). Отсюда следует, что если f вхпо каким-либо причинам получила приращение D f вх(достаточно малое), то приращение D f выхчастоты f выхтаково, что D f вх/ f вх= D f вых/ f вых, т. е. относительная нестабильность частоты колебаний при умножении остаётся неизменной. Это важное свойство У. ч. позволяет использовать их для повышения частоты стабильных колебаний (обычно получаемых от кварцевого задающего генератора ) в различных радиопередающих, радиолокационных, измерительных и др. установках.
Читать дальше

 и
и  определяется равенством
определяется равенством 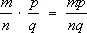 (см. Дробь ) . У. рациональных чисел даёт число, абсолютная величина которого равна произведению абсолютных величин сомножителей, имеющее знак плюс (+), если оба сомножителя одинакового знака, и знак минус (–), если они разного знака. У. иррациональных чисел определяется при помощи У. их рациональных приближений. У. комплексных чисел, заданных в форме a = а + bi и b = с + di, определяется равенством ab = ac – bd + ( ad + bc ) i. При У. комплексных чисел, записанных в тригонометрической форме:
(см. Дробь ) . У. рациональных чисел даёт число, абсолютная величина которого равна произведению абсолютных величин сомножителей, имеющее знак плюс (+), если оба сомножителя одинакового знака, и знак минус (–), если они разного знака. У. иррациональных чисел определяется при помощи У. их рациональных приближений. У. комплексных чисел, заданных в форме a = а + bi и b = с + di, определяется равенством ab = ac – bd + ( ad + bc ) i. При У. комплексных чисел, записанных в тригонометрической форме: