Соч.: Abhandlungen zur Wellenmechanik, 2 Aufl., Lpz., 1928; в рус. пер. — Избр. труды по квантовой механике, М., 1976 (сер. «Классики науки»); Что такое жизнь? С точки зрения физика, 2 изд., М., 1972.
Л. С. Полак.

Э. Шрёдингер.
Шрёдингера уравне'ние,основное динамическое уравнение нерелятивистской квантовой механики ; названо в честь австрийского физика Э. Шрёдингера , который предложил его в 1926. В квантовой механике Ш. у. играет такую же фундаментальную роль, как уравнение движения Ньютона в классической механике и Максвелла уравнения в классической теории электромагнетизма. Ш. у. описывает измерение во времени состояния квантовых объектов, характеризуемого волновой функцией. Если известна волновая функция y в начальный момент времени, то, решая Ш. у., можно найти y в любой последующий момент времени t.
Для частицы массы т , движущейся под действием силы, порождаемой потенциалом V ( х , у , z , t ), Ш. у. имеет вид:
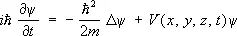 , (1)
, (1)
где i = 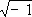 ,
, 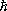 = 1,05 .10 ¾27 эрг . сек — Планка постоянная ,
= 1,05 .10 ¾27 эрг . сек — Планка постоянная , 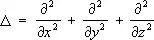 — Лапласа оператор ( х , у , z — координаты). Это уравнение называется временны'м Ш. у.
— Лапласа оператор ( х , у , z — координаты). Это уравнение называется временны'м Ш. у.
Если потенциал V не зависит от времени, то решения Ш. у. можно представить в виде:
y( х , у , z , t ) = 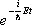 y ( х , у , z ), (2)
y ( х , у , z ), (2)
где Е — полная энергия квантовой системы, а y ( x , у , z ) удовлетворяет стационарному Ш. у.:
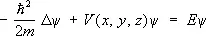 (3)
(3)
Для квантовых систем, движение которых происходит в ограниченной области пространства, решения Ш. у. существуют только для некоторых дискретных значений энергии: E 1 , E 2 , ... , E n ,...; члены этого ряда (в общем случае бесконечного) нумеруются набором целых квантовых чисел n. Каждому значению Е п соответствует волновая функция y n ( x , у , z ), и знание полного набора этих функций позволяет вычислить все измеримые характеристики квантовой системы.
В важном частном случае кулоновского потенциала
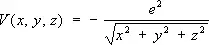
(где е — элементарный электрический заряд) Ш. у. описывает атом водорода, и E n представляют собой энергии стационарных состояний атома.
Ш. у. является математическим выражением фундаментального свойства микрочастиц — корпускулярно-волнового дуализма , согласно которому все существующие в природе частицы материи наделены также волновыми свойствами (эта гипотеза впервые была высказана Л. де Бройлем в 1924). Ш. у. удовлетворяет соответствия принципу и в предельном случае, когда длины волн де Бройля значительно меньше размеров, характерных для рассматриваемого движения, содержит описание движения частиц по законам классической механики. Переход от Ш. у. к классическим траекториям подобен переходу от волновой оптики к геометрической. Аналогия между классической механикой и геометрической оптикой, которая является предельным случаем волновой, сыграла важную роль в установлении Ш. у.
С математической точки зрения Ш. у. есть волновое уравнение и по своей структуре подобно уравнению, описывающему колебания нагруженной струны. Однако, в отличие от решений уравнения колебаний струны, которые дают геометрическую форму струны в данный момент времени, решения y( х , у , z , t ) Ш. у. прямого физического смысла не имеют. Смысл имеет квадрат волновой функции, а именно величина r n ( x , у , z , t ) = |y n ( x , у , z , t )| 2, равная вероятности нахождения частицы (системы) в момент t в квантовом состоянии n в точке пространства с координатами х , у , z. Эта вероятностная интерпретация волновой функции — один из основных постулатов квантовой механики.
Читать дальше


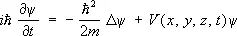 , (1)
, (1)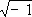 ,
, 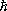 = 1,05 .10 ¾27 эрг . сек — Планка постоянная ,
= 1,05 .10 ¾27 эрг . сек — Планка постоянная , 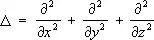 — Лапласа оператор ( х , у , z — координаты). Это уравнение называется временны'м Ш. у.
— Лапласа оператор ( х , у , z — координаты). Это уравнение называется временны'м Ш. у.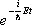 y ( х , у , z ), (2)
y ( х , у , z ), (2)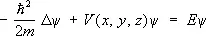 (3)
(3)