Уильям Бернстайн - Разумное распределение активов. Как построить портфель с максимальной доходностью и минимальным риском

Две первые колонки – это годовая доходность и стандартные отклонения. В соседних колонках приведены корреляции между годовой доходностью каждого актива за 27 годовых периодов.

Эти данные вводятся в оптимизатор, в нашем случае MVOPIus, производимый компанией Efficient Solutions. Как и во всех оптимизаторах Марковица, в этой программе используется метод критической линии для создания серии угловых портфелей, которые определяют построение границы эффективности для этого набора исходных данных. Рассмотрим результаты, представленные в табл. 5.2. На рис. 5.1 показаны реальные графические результаты работы MVOPIus.

Угловой портфель 1 – это портфель с минимальным отклонением; его риск минимален. Заметьте, что он состоит на 92,5 % из казначейских векселей и лишь на 7,5 % – из активов, которые мы обычно считаем довольно рискованными. Большинство портфелей в диапазоне риска, который большинство из нас сочло бы обоснованным, находится между угловыми портфелями 7 и 8. Портфели с 1-го по 6-й почти полностью состоят из краткосрочных обязательств, а выше портфеля 8 портфели становятся очень рискованными. Портфель 10 – портфель с максимальной доходностью.

Табл. 5.1. Исходные данные для оптимизатора, 1970–1996 гг.

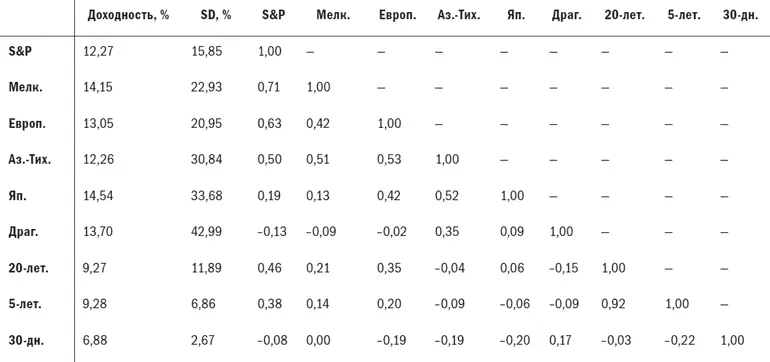
Примечание: S&P-акции S&P 500; Мелк. – акции мелких компаний США (CRSP дециль 9-10); Европ. – акции европейских компаний (MSCI Europe); Аз. – Тих. – акции компаний Азиатско-Тихоокеанского региона (исключая Японию, MSCI Pacific ex-Japan); Япон. – акции японских компаний (MSCI Japan); Драг. – акции компаний, занимающихся добычей драгоценных металлов (объективная категория компании Morningstar); 20-лет. – 20-летние казначейские облигации США; 5-лет. – 5-летние казначейские билеты США; 30-дн. – 30-дневные казначейские векселя США.

Табл. 5.2. Угловые портфели, 1970–1996 гг.

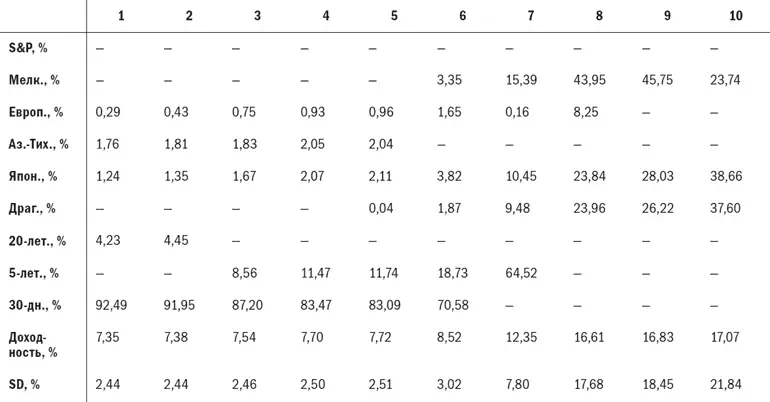
Примечание: S&P – акции S&P 500; Мелк. – акции мелких компаний США (CRSP дециль 9-10); Европ. – акции европейских компаний (MSCI Europe); Аз. – Тих. – акции компаний Азиатско-Тихоокеанского региона (исключая Японию, MSCI Pacific ex-Japan); Япон. – акции японских компаний (MSCI Japan); Драг. – акции компаний, занимающихся добычей драгоценных металлов (объективная категория компании Morningstar); 20-лет. – 20-летние казначейские облигации США; 5-лет. – 5-летние казначейские билеты США; 30-дн. – 30-дневные казначейские векселя США.

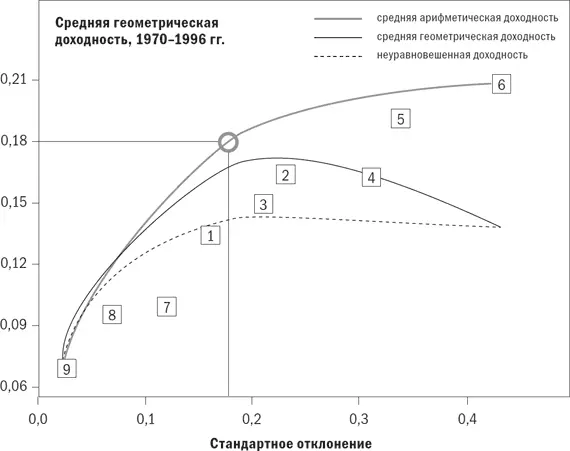
Рис. 5.1. Выходные данные оптимизатора MVOPlus

Математические подробности

MVOPlus обладает уникальной способностью определения портфеля с максимальной годовой доходностью (средней геометрической доходностью), в то время как все другие коммерческие оптимизаторы определяют актив с самой высокой средней арифметической доходностью в качестве последнего портфеля, который не является портфелем с максимальной средней геометрической доходностью. Это происходит потому, что разница между средней арифметической и средней геометрической доходностью равна примерно половине отклонения портфеля, или (SD) 2/ 2, и называется запаздыванием отклонения (variance drag). По мере движения вправо по графику соотношения доходности и риска запаздывание отклонения возрастает до точки, когда средняя геометрическая доходность начинает падать. Помните, что вы уменьшаете среднюю геометрическую доходность в годовом исчислении, а не среднюю арифметическую доходность.

Конечно, вы не ограничены угловыми портфелями. Если вы решите, что хотите оказаться на середине пути между портфелями 7 и 8, то просто усредняйте составы двух портфелей для каждого актива.

Взгляните на портфель 7. Он примерно на треть состоит из акций и на две трети из 5-летних казначейских билетов. Пока все вроде бы нормально. Но посмотрите на состав акций: почти исключительно акции мелких компаний США, японских компаний и компаний, занимающихся добычей драгоценных металлов. Это не тот портфель, которым хотел бы владеть любой разумный человек. Неслучайно в него вошли три актива, по которым получена самая высокая доходность за период с 1970 по 1996 г. Мы только что столкнулись с губительным недостатком оптимизации – излишним пристрастием к активам, имеющим в последнее время высокую доходность. По сути, после небольшой практики можно добиться от оптимизатора расчета почти любого желаемого портфеля. Измените данные о доходности по большинству активов на несколько процентов в любом направлении, и этот актив будет либо доминировать в портфеле, либо полностью исчезнет из него. Вы думаете, что можете спрогнозировать доходность по всем основным классам активов в своем портфеле? Если да, то вы и в самом деле очень талантливы. Следовательно, два фундаментальных закона оптимизаторов: