Эдвард де Боно - Курсы развития мышления

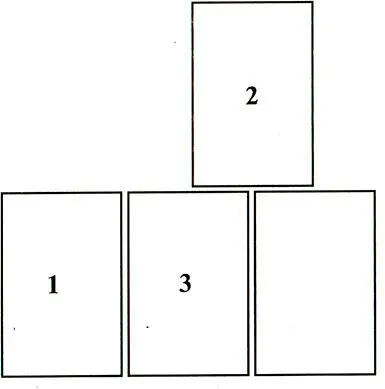
Рис. 18. Комбинация из четырех блоков с одним, двумя и тремя контактами

Затем необходимо добавить пятый блок так, чтобы один из блоков имел четыре контакта с другими. Решение для этого этапа изображено на рис. 19.

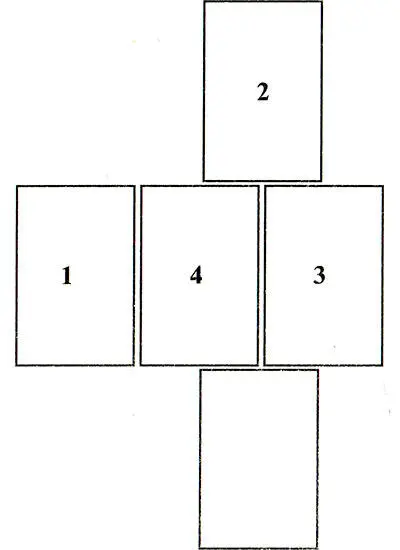
Рис. 19. Комбинация из пяти блоков с одним, двумя, тремя и четырьмя контактами

И, наконец, последний этап — размещение шестого блока с пятью контактами. Решение здесь можно получить столь же легко, как и на предыдущих этапах. Окончательное решение изображено на рис. 20. Лишь при таком методичном подходе задача не кажется чрезмерно сложной.

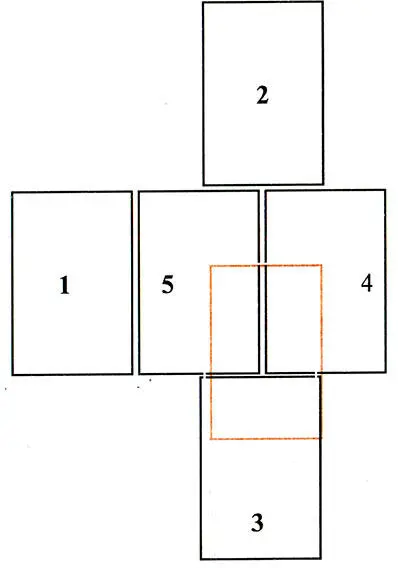
Рис. 20. Решение задачи 5, демонстрирующее число контактов от одного до пяти

Вместо поэтапного метода вы могли прибегнуть к преобразованию предыдущих решений. Один из весьма интересных способов состоит в использовании решения задачи 4 (см. рис. 17) с модификацией его «методом вычитания». Так как в этой комбинации каждый блок касается пяти других, то идея заключается в уменьшении числа контактов отдельных блоков последовательно, пока оно не составит 1, 2, 3, 4 и 5. Сначала снимем один из верхних блоков и приставим его к одиночному нижнему. Теперь этот нижний блок будет по-прежнему касаться пяти, а остальные — четырех других блоков. Затем снимем один верхний блок и разместим его так, чтобы у блока с пятью контактами их число не изменилось, как и у одного из блоков с четырьмя контактами. Количество контактов оставшегося верхнего блока будет равно трем. Перемещенные вниз блоки имеют один и два контакта соответственно. Задача решена. Окончательная комбинация блоков показана на рис. 21. В ней последний верхний блок слегка повернут. Итак, посредством перемещения всего двух блоков решение задачи 4 превращается в решение задачи 5.

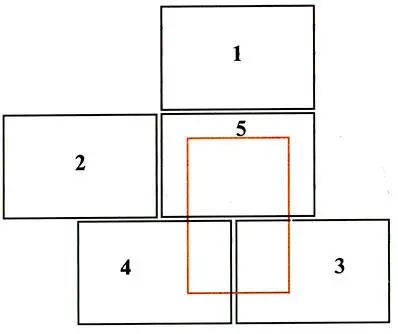
Рис. 21. Решение задачи 5, полученное из решения задачи 4

Возможны и другие пути решения этой задачи. Для вас представляет интерес проанализировать выбранный вами метод, насколько он отличается от описанных здесь. Маловероятно, что в данном случае вы нашли лучшие подходы.

Тем из вас, кто не пренебрегает моими комментариями, скажу следующее.

1. Сложные задачи иногда можно решать «по кусочкам». Их условия выполняются последовательно. Этот метод можно назвать поэтапным.

2. Если решение состоит из взаимосвязанных частей, поэтапный метод вам не поможет.

3. При поэтапном методе определяющим является выбор последовательности рассматриваемых стадий. Неверный выбор такой последовательности может завести вас в тупик, верный же не всегда очевиден.

4. Рассмотрение сложной задачи с различных точек зрения иногда способствует ее упрощению.

5. Решение сложной задачи может быть последовательно выведено из решения более простой задачи.

6. Даже если связь новой задачи с предыдущими не очевидна, можно попытаться модифицировать уже известные решения.

7. Модификация «методом вычитания» состоит в последовательном упрощении решения более сложной задачи.

Обдумывая эти задачи, вы, вероятно, пришли к мнению, что процесс мышления иногда довольно беспорядочен. Возможно, вы предпочли описанные в книге логические подходы или определили их уже после того, как задача была решена. Если ваш подход, хотя и не абсолютно четкий, оказался все же эффективным, вы узнаете намного больше об особенностях своего мышления, нежели человек, облачающий свой случайный успех в мантию логики.

Логический подход обеспечивает, конечно, быстроту и эффективность решения задач (за исключением тех из них, которые требуют генерирования новых идей). К сожалению, практическое мышление далеко уходит от академических рассуждений. Случай, опыт, предрассудки — все оказывает тут влияние. Любопытно, что для решения некоторых проблем при помощи компьютера программы делают лишь частично логичными.

Так как неупорядоченное мышление является скорее приобретенным навыком, не зависящим от математических способностей индивидуума, его можно совершенствовать посредством упражнений и самоанализа (как в задачах этих курсов).