Айван Пастин - Теория игр в комиксах

Может показаться странным, что мы связываем с числовыми показателями понятия благосостояния и приспособленности животного. Однако на решения игроков влияют не столько сами числа, сколько то, как эти числа соотносятся.

Для стратегического взаимодействия двух студий важны лишь их предпочтения относительно исхода. Нам важно знать лишь то, какие результаты лучше, а какие хуже для каждого из участников. Числа – это просто удобный способ представления этих предпочтений.

Конечно, существует множество значимых ситуаций, в которых людям важны не только свои собственные выигрыши, но и чужие. Друзья и члены семьи, как правило, стараются радовать друг друга, а пары в состоянии развода и деловые конкуренты могут быть не против причинить друг другу неприятности.

Подобные ситуации легко поддаются анализу с помощью теории игр: записывая потенциальные выигрыши, мы учитываем все желания участников, включая и желания, связанные с личной выгодой, и желание помочь или навредить другим. Значащиеся в таблице числа – это итоговый выигрыш, который каждый из игроков получит при любом из исходов: так, выгода, которую участник способен извлечь, может быть прямой или непрямой (например, если он причинит вред или поможет кому-либо). Таким образом, выигрыш учитывает все, что для человека важно.

Соответственно, в игре стратегической формы каждый игрок заинтересован лишь в увеличении своих выигрышей.

Теперь, когда мы уточнили условия игры, записав ее в стратегической форме, можем перейти к возможным последующим событиям.

Равновесие Нэша – это фундаментальная концепция в теории игр, названная в честь американского математика Джона Нэша(1928–2015). Само понятие математического равновесия было придумано задолго до Нэша, но он был первым, кто приложил его к математическому анализу игр в общем, а не только к отдельным примерам, как делали раньше.

Идея равновесия Нэша и достаточно проста, и эффективна одновременно: в ситуации равновесия каждый рациональный игрок выбирает свою оптимальную стратегию, учитывая, что другой игрок также придерживается определенной стратегии. То есть участник выбирает стратегию в зависимости от действий оппонента.

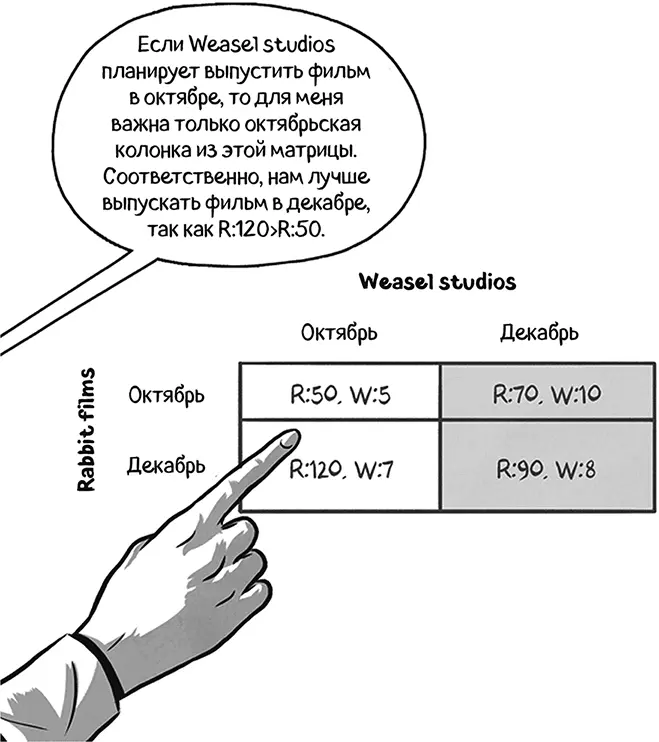
Оптимальная стратегия Rabbit films

• Если Rabbit films ожидает, что Weasel Studios выпустит фильм в октябре, то их оптимальной стратегией будет выпуск фильма в декабре, так как R:120 > R:50. Подчеркиваем R:120.

• Если Rabbit films ожидает, что Weasel Studios выпустит фильм в декабре, то их оптимальной стратегией будет выпуск фильма в декабре, так как R:90 > R:70. Подчеркиваем R:90.

Оптимальная стратегия Weasel studios

• Если Weasel Studios ожидает, что Rabbit films выпустит фильм в октябре, то их оптимальной стратегией будет выпуск фильма в декабре, так как W:10 > W:5. Подчеркиваем W:10.

• Если Weasel Studios ожидает, что Rabbit films выпустит фильм в декабре, то их оптимальной стратегией будет выпуск фильма в декабре, так как W:8 > W:7. Подчеркиваем W:8.

В ситуации равновесия обе студии выпустили бы фильмы в декабре. Это единственный исход, при котором оптимальные стратегии обеих студий позволяют достичь наилучших результатов.

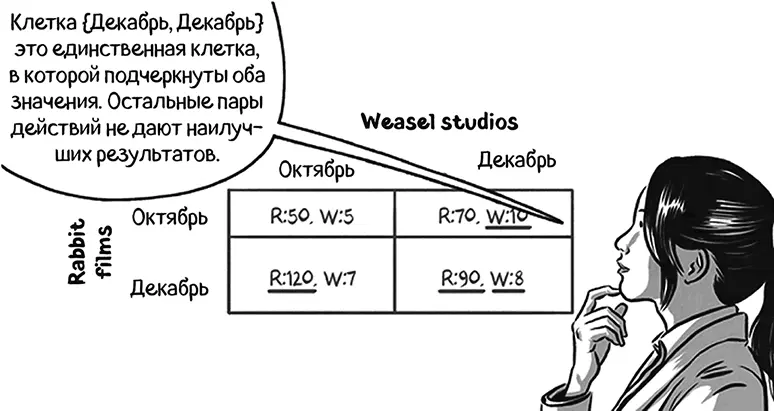
Одной из характеристик равновесия Нэша является отсутствие сожаленияу каждого из игроков. Отказ от стратегии равновесия, подразумевающей выпуск фильмов в декабре, не принес бы ни одной из студий никакой выгоды. Равновесие Нэша также является и равновесием рациональных ожиданий. В такой ситуации Rabbit films выпускает фильм в прокат в декабре, ожидая, что Weasel Studios собирается выпускать фильм в прокат в декабре. И действительно, Weasel Studios назначает релиз на декабрь. Соответственно, ожидания правильны.