Айван Пастин - Теория игр в комиксах

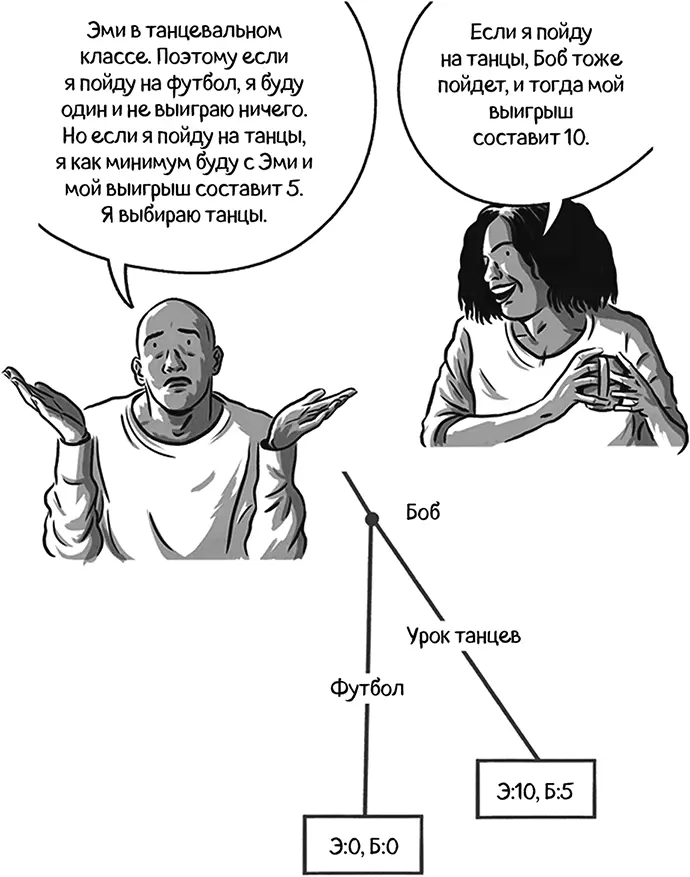
Динамическая игра Эми и Боба может быть разрешена с помощью обратной индукции. Эми предугадывает, что произойдет в конце игры, и распутывает всю игровую цепочку оттуда, пытаясь понять, каким будет ее оптимальный выбор.

С точки зрения Эми было бы рациональным пойти танцевать, так как она знает, что Боб присоединится к ней. Это равновесие, совершенное по под-играм: игроки делают оптимальные для них обоих выборы в каждой под-игре изначальной игры. Равновесие, совершенное по под-играм, означает, что игроки концентрируются на будущем. На каждой точке принятия решения они делают все возможное, не тая обид за прошлые действия.

В этой игре равновесие, совершенное по под-играм, особенно выгодно для Эми. Здесь проявляется преимущество первого хода.

Однако не все игры с последовательными ходами имеют такую черту, как преимущество первого хода. Существует множество игр, в которых первый ход ставит игрока в сложное положение.

Большинство людей считают, что равновесие Нэша, совершенное по под-играм, при котором оба участника идут на урок танцев, это самое вероятное равновесие, однако существуют и другие равновесия.

К примеру, Боб мог заявить, что он всегда будет ходить на футбол, вне зависимости от того, чего хочет Эми. Если Эми верит этому, то она будет ожидать провести этот вечер в одиночестве, если выберет урок танцев. Поэтому она тоже пойдет на футбол, ведь быть с Бобом ей нравится больше, чем быть одной. Это тоже равновесие Нэша, но оно основывается на вере Эми в то, что Боб действительно пойдет на футбол, даже если она позвонит ему из класса. Это не входит в интересы Боба, поэтому его угроза недостоверна.

Равновесие, совершенное по под-играм, не обращает внимания на равновесия Нэша, которые зависят от недостоверных угроз или обещаний.

Взаимодействие между кредиторами и заемщиками могут быть смоделированы в виде игры с последовательными действиями. Это может быть полезно при анализе причин того, почему многообещающие проекты не получают финансирования.

Расширенная форма игры моделирует ожидаемые выигрыши (прибыль в миллионах фунтов) для потенциального заемщика (А) и банка (Б). Для упрощения предположим, что банк и заемщик прекрасно понимают, как работают игровое дерево и ожидаемые выигрыши.

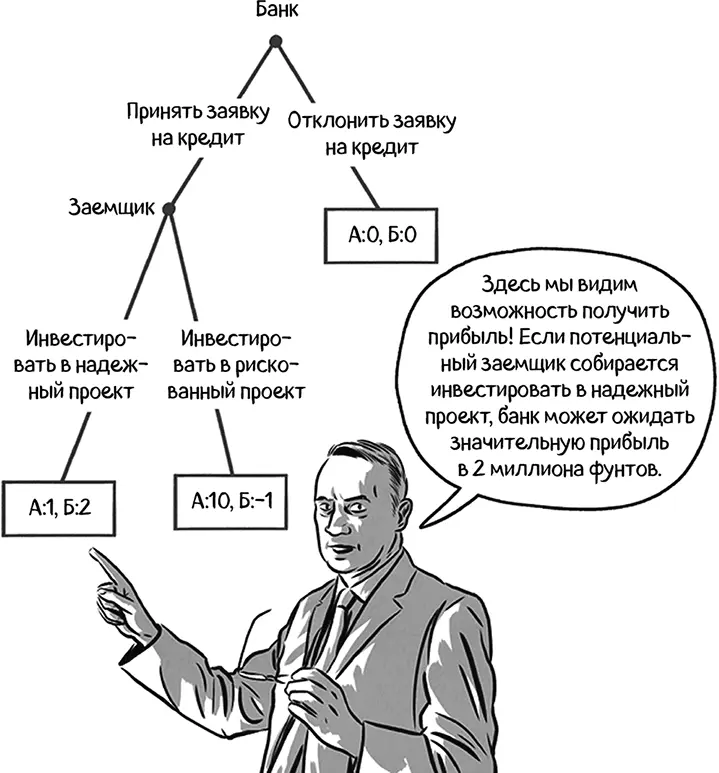
У заемщика есть выбор: инвестировать в надежный или в ненадежный проект, но это будет возможно, только если кредит будет одобрен банком.

Банк предпочел бы, чтобы заемщик инвестировал в надежные проекты. Тем не менее он не может отслеживать ежедневную деятельность заемщика. Значит, он не может указывать, в какой проект можно инвестировать, а в какой нет. В равновесии, совершенном по под-играм, банковский работник отказывает заемщику в кредите, хотя и банк, и сам заемщик извлекли бы значительную выгоду из прибыльного надежного проекта.

Заемщик может пообещать работнику банка, что будет вкладывать средства в надежный проект. И он даже может говорит от чистого сердца, ведь в случае отклонения заявки его выигрыш составит ноль, но если кредит будет одобрен, получит выигрыш, равный 1 миллиону фунтов.

Тем не менее если бы банк одобрил этот кредит, то, как только заемщик получил бы деньги, он бы стал сравнивать ожидаемый выигрыш от надежного проекта с ожидаемым выигрышем от рискованного проекта. Так, он бы выбрал рискованный проект и тем самым нарушил бы свое обещание. Такой случай носит название « проблема несогласованности во времени»: человек, принимающий решение, не может не отступить от изначального плана действий.

Равновесие, совершенное по под-играм, при котором банк отклоняет заявку на кредит, не эффективно по Парето. И банковский работник, и заемщик извлекли бы большую выгоду, если бы в надежный проект были вложены средства.