Стивен Питчер - Сакральное значение чисел. Духовные истины на языке математики

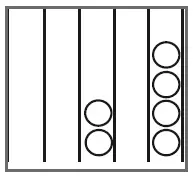
Рис. 1. Число 204, отложенное на счетах

На рис. 1 показано, как на счетах выглядело число 204. Как бы ни было важно поместное значение чисел при операциях на счетах, эту технику не включали в работу с написанными числами вплоть до XV века.

Весьма любопытно, что в Китае вместо костяшек в счетах использовали маленькие деревянные или бамбуковые палочки. Возможно, это связано с тем, что изначально при работе с «И-Цзином» («Книгой Перемен») пользовались именно палочками. Сегодня для простоты вместо палочек кидают три монеты. И-Цзин базируется на 64 гексаграммах. Гексаграмма – это шесть линий, которые могут быть прерывистыми или сплошными (рис. 2). При истолковании смысл гексаграммы определяют по конкретному сочетанию линий и порядку их расположения. Чередование прерывистых и сплошных линий наводит на мысль о древней китайской двоичной системе счисления, поскольку мы имеем лишь два символа. Это еще один пример того, как древние народы использовали математику для выражения концепций мудрости и духовности.

Рис. 2. Эта взятая в качестве примера гексаграмма по номером 17 называется Суй («Следование»). Ее краткое истолкование звучит следующим образом: «Радость движения ведет к следованию. Идея следования как приспособление к велениям времени произрастает из этого образа»

Значительный прогресс в написании чисел произошел, когда в качестве числовых систем стали использовать алфавиты. Это изобретение греки сделали примерно за 450 лет до нашей эры, а потом его переняли древние иудеи. В алфавитах обоих народов первые девять букв выступали также в качестве цифр от 1 до 9. Следующие девять букв представляли десятки, от 10 до 90, а последние девять были сотнями, от 100 до 900. Колоссальным преимуществом таких алфавитных чисел была простота. До появления алфавитных чисел письменные знаки существовали только для 1, 5, 10, 100 и так далее. Остальные числа писали, повторяя и комбинируя эти базовые цифры. Точно так же как на счетах, 4, например, записывали, четыре раза написав «1»; 40 записывали в виде значка 10, повторенного четыре раза. Давайте рассмотрим конкретный пример. В Древнем Египте 1 представляла собой вертикальную линию, а 10 – арку. Вот как они изображали число 44: ││││∩∩∩∩. Алфавитные же числа предлагали букву/число для всех единиц, десятков и сотен. Поэтому 44 можно было написать как 404 (используя, естественно, соответствующие греческие буквы или буквы иврита). Чтобы написать число 404, что мы сейчас делаем, вставив 0, эти народы писали 4004, и при этом не испытывали ни малейших страданий по поводу того, что в столбце десятков у них ничего не стояло. «Для примитивного человека, делающего подсчеты, число – это всегда число, количество, и только число может иметь символ» [10] Karl Meninger. Number Words and Number Symbols: A Cultural History of Numbers (Cambridge, Mass.: The M.l.T. Press, 1970), p. 400. Joseph Campbell. The Masks of God (New York: Penguin Books, 1976), p. 185. . Именно так и поступали древние египтяне и большинство других древних народов, и точно так же они проделывали это на счетах. Египтяне обозначали число 100 как 9, поэтому 404 они писали так: ││││9999. Благодаря алфавитным числам впервые стало возможно использовать написанные числа для совершения подсчетов, какими бы неуклюжими и громоздкими они не казались нам сейчас.

Алфавитные числа явно стали предтечей современной нумерологической практики приписывать буквам числовые значения, в том числе пифагорейской и каббалистической нумерологии. На первых порах алфавитные числа были чисто математической разработкой. Однако вскоре символизм чисел распространился на буквы и слова, составленные из этих букв. Числовой символизм, подобно всем духовным символическим системам, склонен развиваться в двух направлениях. Во-первых, система символов медленно созревает по мере того, как с ней работают, поколение за поколением, представители данной культуры. Постепенно обветшалые элементы подвергаются ректификации и очищению благодаря многократным пересказам. Происходит своеобразный органический процесс отсева, благодаря которому базовые истины о человеческой природе и жизни принимают чистую, архетипическую форму. Однако в какой-то момент эта достойная работа приносит в жертву систему символов, порождая мудрость и духовное знание священного характера. При развитии во втором направлении какой-нибудь одаренный индивид делает настолько глубокий и важный вклад во всю систему символов, что та приобретает глубокое видение и пророческие возможности.