Александр Матанцев - Пирамиды – источники огромной энергии по древним технологиям и возможности сейчас

К первой категории относятся осевые (аксиальные) волны. Их подразделяют на три класса: продольные, поперечные и вертикальные. Звуковые волны каждого из этих классов отражаются только от двух противоположных стен (или от потолка и пола). Ко второй категории относятся касательные волны, которые распространяются, последовательно отражаясь от четырех стен. Последняя категория – так называемые косые волны, отражающиеся последовательно от всех шести ограждающих поверхностей.

Очевидно, что бороться с самим фактом возникновения резонансов в помещении тяжело, а зачастую и не нужно – если резонансы расположены в заданной полосе частот близко друг к другу и равномерно, то форма сигнала в этой полосе частот передается практически без искажений.

Физик-теоретик Филипп Морз вывел формулу для подсчета количества резонансных частот в заданном диапазоне частот в зависимости от объема и линейных размеров помещения [44], откуда видно, что количество резонансов помещения, приходящихся на одну и ту же полосу частот, с понижением частоты существенно уменьшается. Морз подсчитал, сколько в помещении должно быть резонансов в заданном интервале частот для того, чтобы без заметных искажений нести форму звука длительностью порядка 0,1 с. Результат его расчетов таков: в интервале Δf=10 Гц должно быть не менее 10 резонансов.

Если механическая волна, распространяющаяся в среде, встречает на своем пути какое-либо препятствие, то она может резко изменить характер своего поведения. Например, на границе раздела двух сред с разными механическими свойствами волна частично отражается, а частично проникает во вторую среду. Волна, бегущая по резиновому жгуту или струне отражается от неподвижно закрепленного конца; при этом появляется волна, бегущая во встречном направлении. В струне, закрепленной на обоих концах, возникают сложные колебания, которые можно рассматривать как результат наложения (суперпозиции) двух волн, распространяющихся в противоположных направлениях и испытывающих отражения и переотражения на концах. Колебания струн, закрепленных на обоих концах, создают звуки всех струнных музыкальных инструментов. Очень похожее явление возникает при звучании духовых инструментов, в том числе органных труб.

Если волны, бегущие по струне во встречных направлениях, имеют синусоидальную форму, то при определенных условиях они могут образовать стоячую волну.

Пусть струна длины l закреплена так, что один из ее концов находится в точке x = 0, а другой – в точке x 1 = L (рис. 31). В струне создано натяжение T.

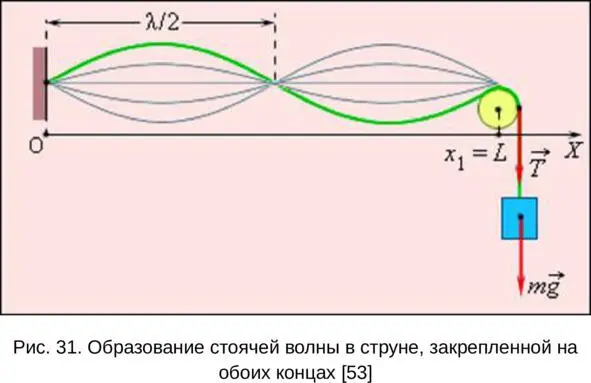
Рис. 31.

По струне одновременно распространяются в противоположных направлениях две волны одной и той же частоты:

y 1 (x, t) = A cos (ωt + kx) – волна, бегущая справа налево;

y 2 (x, t) = —A cos (ωt – kx) – волна, бегущая слева направо.

В точке x = 0 (один из закрепленных концов струны) падающая волна y 1в результате отражения порождает волну y 2. При отражении от неподвижно закрепленного конца отраженная волна оказывается в противофазе с падающей. Согласно принципу суперпозиции, который является экспериментальным фактом, колебания, вызванные встречными волнами в каждой точке струны, складываются. Таким образом, результирующее колебание в каждой точке равно сумме колебаний, вызванных волнами y 1и y 2в отдельности. Следовательно,

Это и есть стоячая волна. В стоячей волне существуют неподвижные точки, которые называются узлами. Посередине между узлами находятся точки, которые колеблются с максимальной амплитудой. Эти точки называются пучностями.

Оба неподвижных конца струны должны быть узлами. Приведенная выше формула удовлетворяет этому условию на левом конце (x = 0). Для выполнения этого условия и на правом конце (x = L), необходимо чтобы kL = nπ, где n – любое целое число. Это означает, что стоячая волна в струне возникает не всегда, а только в том случае, если длинаL струны равняется целому числу длин полуволн: l = n (λ n/2) λ n= 2l/n (n = 1,2,3…)

Набору значений λn длин волн соответствует набор возможных частот fn:

f n= v/ λ n

где v = √T/μ— скорость распространения поперечных волн по струне. Каждая из частот f N и связанный с ней тип колебания струны называется нормальной модой. Наименьшая частота f 1называется основной частотой, все остальные (f 2, f 3, …) называются гармониками. На рис. 32 изображена нормальная мода для n = 2, а на рис. 33 показаны гармоники.