Михаил Заречный - Квантово-мистическая картина мира. Структура реальности и путь человека

Но, может быть, электроны каким-то образом блуждают от отверстия к отверстию и только потом достигают детектора? Это объяснение также не подходит: на кривой P 12при двух открытых щелях есть точки, в которые попадает значительно меньше электронов, чем при любой из открытых щелей. И наоборот, есть точки, вероятность попадания электронов в которые более чем вдвое превышает вероятность попадания электронов, прошедших через каждую щель по отдельности.

Стало быть, утверждение о том, что электроны проходят либо сквозь щель 1, либо сквозь щель 2, неверно. Они проходят через обе щели одновременно. И очень простой математический аппарат, описывающий такой процесс, дает абсолютно точное согласие с экспериментом, показанным сплошной линией на графике.

Если подойти к вопросу более строго, то утверждение, что электрон проходит одновременно через две щели, неверно. Понятие «электрон» можно соотнести только с локальным объектом (смешанным, «проявленным» состоянием), здесь же мы имеем дело с квантовой суперпозицией различных компонент волновой функции.

Чем же отличаются пули от электронов? С точки зрения квантовой механики — ничем. Только, как показывают расчеты, интерференционная картина от рассеяния пуль характеризуется столь узкими максимумами и минимумами, что никакой детектор их зарегистрировать не в состоянии. Расстояния между этими минимумами и максимумами неизмеримо меньше размеров самой пули. Так что детекторы будут давать усредненную картину, показанную сплошной кривой на рис. 1.

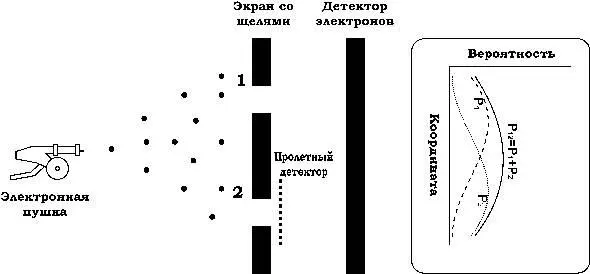
Давайте теперь внесем такие изменения в эксперимент, чтобы можно было «проследить» за электроном, то есть узнать, через какую щель он проходит. Поставим возле одной из щелей детектор, который регистрирует прохождение электрона сквозь нее (рис. 3).

В этом случае, если пролетный детектор регистрирует прохождение электрона через щель 2, мы будем знать, что электрон прошел через эту щель, а если пролетный детектор не дает сигнала, а основной детектор дает сигнал, то ясно, что электрон прошел через щель 1. Можно поставить и два пролетных детектора — на каждую из щелей, но это никак не скажется на результатах нашего опыта. Конечно, любой детектор, так или иначе, исказит движение электрона, но будем считать это влияние не очень существенным. Для нас ведь куда более важен сам факт регистрации того, через какую из щелей проходит электрон!

Как вы думаете, какую картину мы увидим? Результат эксперимента показан на рис. 3, качественно он ничем не отличается от опыта с пулеметной стрельбой. Таким образом, мы выяснили, что, когда мы смотрим на электрон и фиксируем его состояние, то он проходит либо через одно отверстие, либо через другое. Суперпозиции этих состояний нет! А когда мы на него не смотрим, электрон одновременно проходит через две щели, и распределение частиц на экране совсем не такое, как тогда, когда мы на них смотрим! Выходит, наблюдение как бы «вырывает» объект из совокупности неопределенных квантовых состояний и переводит его в проявленное, наблюдаемое, классическое состояние.

Может быть, всё это не так, и дело только в том, что пролетный детектор слишком сильно искажает движение электронов? Проведя дополнительные опыты с различными детекторами, по-разному искажающими движение электронов, мы заключаем, что роль этого эффекта не очень существенна. Существенным оказывается только сам факт фиксации состояния объекта!

Таким образом, если измерение, проведенное над классической системой, может и не оказать никакого влияния на ее состояние, для квантовой системы это не так: измерение разрушает чисто квантовое состояние, переводя суперпозицию в смесь.

Сделаем математическое резюме полученных результатов. В квантовой теории вектор состояния принято обозначать символом | >. Если какой-то набор данных, определяющих систему, обозначить буквой x, то вектор состояния будет иметь вид |x>.

В описанном эксперименте при открытой первой щели вектор состояния обозначается как |1>, при открытой второй щели — как |2>, при двух открытых щелях вектор состояния будет содержать две компоненты,

|x> = a|1> + b|2>, (1)

где a и b — комплексные числа, называемые амплитудами вероятности. Они удовлетворяют условию нормировки |a| 2 + |b| 2 = 1.

В случае, если поставлен пролетный детектор, квантовая система перестает быть замкнутой, поскольку с ней взаимодействует внешняя система — детектор. Происходит переход суперпозиции в смесь, и теперь вероятности прохождения электронов через каждую из щелей даются формулами P 1 = |a| 2 , P 2 = |b| 2 , P 1 + P 2 = 1. Интерференция отсутствует, мы имеем дело со смешанным состоянием.