Вильгельм Оствальд - Искусство цвета. Цветоведение - теория цветового пространства

Необходимо каждую из них разделить, следуя десятичной системе, еще на 10 ступеней. Эти ступени можно найти, если взять числа, соответствующие логарифмам, равным 1,000, 0,900, 0,800, 0,700, 0,600…0,100 и принять наибольшее из них за 1. Таковыми окажутся в результате числа 1,00, 0,79, 0,63, 0,50, 0,40, 0,32, 0,25, 0,16, 0,125, 0,100. Если вставим десять ступеней между 0,100 и 0,010, то найдем эти же числа, только в десять раз уменьшенные. То же повторится между 0,010 и 0,001 и т. д. Так как разница между двумя ступенями в среднем составляет около 20 %, то она лежит значительно выше порога, а потому ощутима. Дальнейшее деление на десять новых, более мелких ступеней, неприемлемо, так как разница между этими делениями будет лежать уже ниже порога различения.

Данные величины делят непрерывный серый ряд на одинаково отстоящие для нашего восприятия отрезки. Нам же нужны не отрезки, а точки – т. е. определенные серые цвета. Эти цвета мы и можем получать посредством смешения всех цветов каждого данного отрезка ряда. Соответствующие им числа суть средние геометрические двух граничных чисел. Мы получаем, таким образом, следующий ряд, который обозначаем сокращенно, как было указано выше, цифрами, показывающими процентное содержание белого цвета:

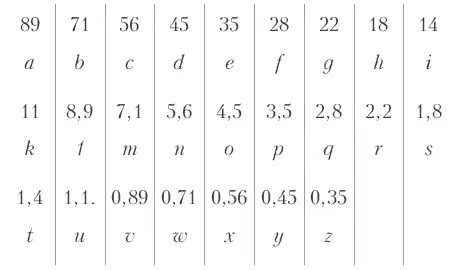
Мы заканчиваем наш ряд на 0,35, так как очень мало таких поверхностей, которые бы отражали света так мало или еще меньше. Теоретически можно продолжать этот ряд до бесконечности. Под числами находятся буквы латинской азбуки, которые обозначают ступени серого ряда, так же, как в музыке тона обозначаются буквами. Каждая буква может обозначать написанное над нею количество белого света (в процентах) или количество черного цвета, если возьмем число дополнительное до 100. Таким образом, буква i может означать 14 % белого цвета или 86 % черного. На практике для большинства случаев эти деления еще слишком мелки. Поэтому мы из каждых двух чисел опускаем одно и получаем практический серый ряд (шкалу бело-черного). Мы обрываем его на букве р, так как у буквы р находится самый глубокий черный цвет, который можно получить на бумаге при помощи типографской черной туши:

На прилагаемой таблице № 1 эти ступени а с е g i l n p и представлены. Очень хорошо было бы заучить их наизусть, для того чтобы можно было различать ступени серых цветов: и не имея перед глазами масштаба для сравнения. Для неопытного человека, который ничего не знает о расположении цветов, мысль о таком заучивании покажется абсурдом. Но нужно только попробовать это сделать, чтобы убедиться в ее осуществимости. Такое заучивание совершенно осваивает нас с миром ахроматических цветов.

Приведенный выше геометрический ряд серых цветов начинается с идеально-белого цвета, который вполне определяется условиями полного отражения и рассеивания. Хотя И. Ламберт еще в XVII веке дал такое определение белому цвету и это определение нашло свое применение и в других отраслях науки, как, например, в астрономии, – для авторов, работающих в области науки о цветах, оно осталось но сей день чуждым. Даже Геринг приводит хорошо известный опыт (с отражением дневного света от посеребренного покровного стеклышка, лежащего на белой бумаге) – имеющий целью доказать, что белый цвет можно усиливать безгранично. Мы тут наталкиваемся на ошибочное смешение белого цвета с блеском. Посеребренное покровное стеклышко не рассеивает свет, а только отражает его; оно поэтому не белое, а блестящее.

Несколько иначе проявляет себя черный конец ряда. Первый, описанный нами выше, ахроматический ряд был расположен непосредственно по степеням светлоты и носит поэтому название аналитического ряда и заканчивается черным цветом со светлотой, равняющейся нулю. Такой черный цвет мы можем всегда воспроизвести в отверстии ящика, окрашенного изнутри в черный цвет. Не существует, однако, ни одного такого красящего вещества, которое дало бы этот черный цвет, в чем мы легко убеждаемся, когда сравниваем различные черные окраски с таким отверстием вычерненного внутри ящика. Составленный согласно закону Фехнера геометрический ряд выражает этот факт тем, что совершенно черный цвет является в нем бесконечно удаленным. Сколько бы мы ни продолжали этот ряд, всегда можно прибавить еще одну ступень, которая была бы меньше предыдущей в определенном количественном отношении.