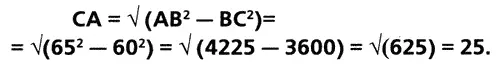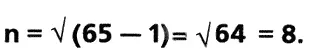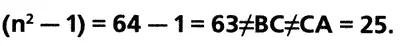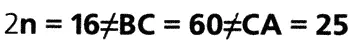Марк Хэддон - Загадочное ночное убийство собаки

И потом я получу Почетную Степень Первого Класса и стану ученым.

Я знаю, что смогу это сделать, потому что я сумел самостоятельно съездить в Лондон и потому что я сумел выяснить, кто убил Веллингтона. Еще я нашел свою мать, я был смелым, я написал книгу, и это значит, что я могу все.

Вопрос

Докажите, что:

треугольник со сторонами, которые могут быть выражены формулами n 2+ 1, n 2 — 1и 2n(где n > 1) является прямоугольным.

Докажите, что обратное утверждение неверно.

Ответ

Сперва мы должны определить, какова самая длинная сторона треугольника со сторонами, которые выражены формулами n 2+ 1, n 2 — 1и 2n(где n > 1).

n 2+ 1 — 2n = (n — 1) 2.

Если n > 1, то (n — 1) 2 > 0.

Следовательно, n 2+1 — 2n > 0.

Следовательно, n 2+ 1 > 2n.

Сходным образом (n 2+1) — (n 2 — 1) = 2.

Следовательно, n 2+ 1 > n 2 — 1.

Это значит, что n 2+ 1является самой длинной из сторон треугольника со сторонами, которые могут быть выражены формулой n 2+ 1, n 2 — 1и 2n(где n > 1).

Для наглядности можно показать это на следующем графике (хотя это ничего не доказывает):

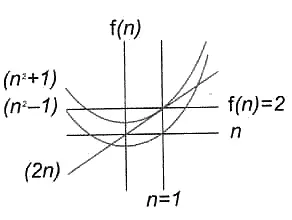
Согласно теореме Пифагора, если сумма квадратов катетов (двух более коротких сторон) равна квадрату гипотенузы (длинной стороны), треугольник является прямоугольным. Следовательно, чтобы доказать, что треугольник прямоугольный, нам нужно показать, что это тот самый случай.

Сумма квадратов двух более коротких сторонравна (n 2 — 1) 2+ (2n) 2.

(n 2 — 1) 2+ (2n) 2= n 4 — 2n 2+ 1 + 4n 2= n 4+ 2n 2+ 1.

Квадрат гипотенузы равен (n 2+1) 2.

(n 2+ 1) 2= n 4+ 2n 2+ 1.

Таким образом, сумма квадратов коротких сторон равна квадрату длинной стороны. Следовательно, треугольник является прямоугольным.

А утверждение, обратное утверждению: «Треугольник со сторонами, которые могут быть выражены формулами n 2+ 1, n 2 — 1и 2n(где n >1) прямоугольный», — это: «Прямоугольный треугольник имеет стороны, которые могут быть выражены формулами n 2+ 1, n 2 — 1и 2n(где n > 1)».

И это значит, что нужно найти треугольник, который будет прямоугольным, но стороны которого не могут быть выражены формулами n 2+ 1, n 2 — 1и 2n(где n > 1).

Итак, пусть гипотенуза прямоугольного треугольника АВСбудет АВ.

Пусть АВ = 65.

Пусть ВС = 60.

Тогда

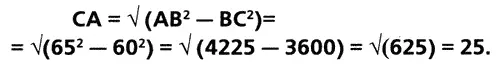
Пусть АВ = n 2+1 = 65.

Тогда

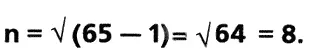
Следовательно,

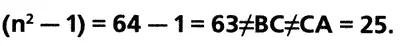
И

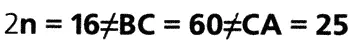
Следовательно, треугольник АВС является прямоугольным, но его стороны не могут быть выражены формулами n 2+ 1, n 2 — 1и 2n(где n > 1). Что и требовалось доказать.

Эту книгу я видел в городской библиотеке, когда мать однажды водила меня с собой в город.

Это не метафора, а образное сравнение. Это значит, что инспектор и правда выглядел так, как будто у него в каждой ноздре прячется мышка. И если вы можете представить себе человека, у которого в ноздрях сидит по мышке, то вы поймете, как выглядел инспектор. А образное сравнение — это не ложь, и это не плохо, если сравнение не обидное.

но у меня не было ни шоколадных подушечек, ни чая, потому что все это коричневое.

Однажды я ни с кем не разговаривал 5 недель.

Когда мне было 6 лет, мать дала мне детского питания с земляничным вкусом. Оно было налито в мерный стакан, и мы соревновались, чтобы понять, как быстро я смогу выпить четверть литра.

Люди утверждают, что нужно всегда говорить только правду. Но на самом деле это не так, поскольку нельзя, например, говорить старым людям, что они старые. Еще нельзя говорить людям, что от них плохо пахнет, когда кто-то, например, пукнул. И еще нельзя говорить человеку: «Ты мне не нравишься», даже если он кажется тебе просто отвратительным.