Марк Хэддон - Загадочное ночное убийство собаки

Мэрилин вос Савант ответила, что нужно переменить решение и выбрать последнюю дверь, поскольку шанс того, что именно за ней будет машина, равен 2 к З.

Если вы воспользуетесь интуицией, то решите, что шансы 50:50, и придете к выводу, что машина может оказаться за любой из двух дверей.

Очень много людей написали в журнал специально для того, чтобы сказать Мэрилин вос Савант, что она неправа. Таких писем было 92 %, и многие из них написаны математиками и другими разными учеными. Вот примеры того, что в них говорилось.

«Я крайне удручен тем фактом, что общественность столь слабо разбирается в математике. Пожалуйста, признайте, что вы неправы.

«Математическая неграмотность просто поражает. И это называется высочайшим уровнем интеллекта. Стыдитесь!

«По крайней мере, три математика указали вам на ошибку. Но вы продолжаете настаивать на своем.

«Могу поспорить, что вы получили множество писем от профессоров и студентов колледжей и высших школ. Рекомендую вам сохранить хотя бы несколько адресов, дабы впоследствии иметь возможность консультироваться с этими людьми.

«Вы категорически неправы… Сколько же нужно разгневанных математиков, чтобы вы переменили мнение?

«Если окажется, что все эти доктора наук были неправы, я сочту, что страна находится в серьезной опасности.

Но Мэрилин вос Савант была права, и существует 2 способа это доказать.

Во-первых, это можно сделать при помощи математики. Вот таким образом:

Назовем двери X, Y и Z.

Пусть С хбудет обозначением того факта, что машина находится за дверью X, — и так далее.

Пусть Н хбудет обозначением того факта, что ведущий открывает дверь X, — и так далее.

Предположим, что вы выбрали дверь X; вероятность того, что вы выиграете машину, если вы перемените свое решение, выражена в следующей формуле:

Р(Н Z^ С Y) + Р(Н Y^ С Z) = Р(С Y). Р(Н Z| С Y) + Р(С Z). Р(Н Y| С Z) = (1/3.1) + (1/3.1) = 2/3.

Второй путь — это проиллюстрировать возможные исходы такой вот таблицей:

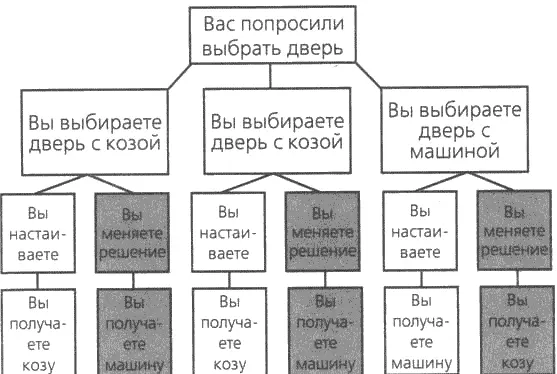
Таким образом, если вы меняете решение, у вас два шанса из трех получить машину. Если же вы настаиваете на первоначальном решении, то у вас один шанс из трех.

И это показывает, что интуиция иногда может быть ошибочной. Интуиция — это то, что люди используют в жизни, чтобы принимать решения. Но найти правильный ответ помогает логика.

И еще это доказывает, что мистер Дживонс был неправ: числа иногда оказываются очень сложными и вовсе не точными. Вот почему мне нравится «Загадка Монти Холла».

Когда я вернулся домой, там был Родри. Родри — это человек, который работает на отца, помогает ему чинить приборы и сантехнику. Иногда он приходит к нам по вечерам, чтобы выпить с отцом пива, посмотреть телевизор и побеседовать.

Родри носит белые рабочие брюки, которые все покрыты грязными пятнами, и золотое кольцо на среднем пальце левой руки. От него пахнет чем-то, что я не знаю, как называется. От отца всегда пахнет так же, когда он приходит с работы.

Я положил свои лакричные палочки и молочную плитку в специальную коробку для еды, которая стоит на полке и которую отцу не разрешается трогать, потому что это мое.

Потом отец спросил:

— И где же это ты гулял, юноша?

Я сказал:

— Зашел в магазин за лакричными палочками и молочной плиткой.

А он ответил:

— Что-то ты долго ходил.

Я сказал:

— Я разговаривал с собакой миссис Александер у магазина. Я погладил ее, и она стала нюхать мои брюки.

И это была еще одна белая ложь.

Потом Родри сказал:

— Боже, ты скоро получишь третью степень, да?

Но я не знаю, что такое третья степень .

А потом он спросил:

— Как дела, капитан?

И я сказал:

— Хорошо, спасибо. — Потому что так нужно отвечать в подобных случаях.

А он спросил:

— Сколько будет, если 251 умножить на 864?

Я немного подумал и сказал:

— 216 864, — потому что это очень просто: нужно умножить 864на 1000, что равно 864 000; потом ты делишь это на 4,что равно 216 000, и это будет то же самое, что 250умножить на 864; потом ты просто прибавляешь 864, чтобы получить 251, умноженное на 864, — получается 216 864. — И я спросил: — Правильно?