Юрий Артамонов - Ли Смолин. Возрожденное время - От кризиса в физике к будущему вселенной

Одной из подсказок было математическое единство двух кривых, описывающих движение. Эллипсы описывают планетарные орбиты, а параболы - пути падающих тел на Земле. Эти два вида кривых тесно связаны. Они оба могут быть получены рассечением конуса плоскостью. Сконструированные таким образом кривые называются коническими сечениями; другими примерами являются окружности и гиперболы.

Вопросом для второй половины 17-го века было открытие физического единства, объясняющего это математическое единство. Догадка, которую выдвинул Ньютон, чтобы вступить в Научную Революцию, касалась природы, а не математики, и не принадлежала ему одному. Несколько его современников осознали великий секрет: Сила, которая

к оглавлению

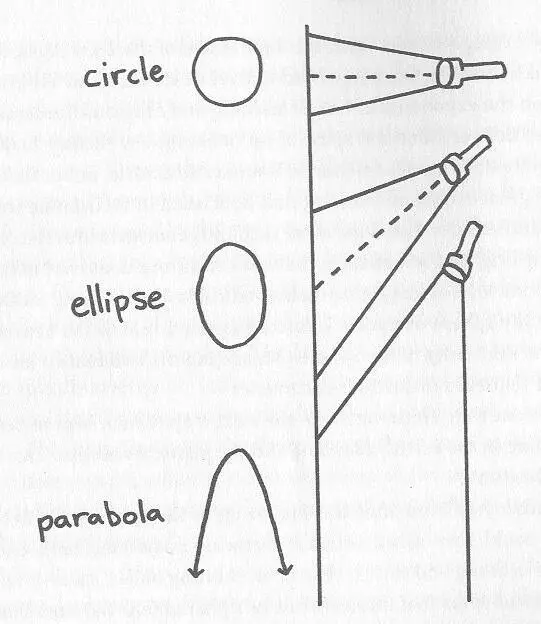Рис.3 . Конические сечения, показанные светом фонарика на стене . заставляет все на Земле падать на нее, универсальна и действует также, притягивая планеты к Солнцу, а Луну к Земле . Гравитация.

Ньютон по легенде получил свое прозрение, сидя в своем саду и наблюдая за падением яблок с дерева, когда он размышлял над движением Луны. Чтобы завершить мысль, он задал другой решающий вопрос: Как эта сила уменьшается с расстоянием между объектами? Она должна уменьшаться, в противном случае нас бы выталкивало вверх к Солнцу, а не вниз к Земле. И как сила производит движение?

Другие, такие как современник Ньютона Роберт Гук, задавали эти вопросы, но успех Ньютона заключался в его правильных ответах

к оглавлению

на них. Ему потребовалось два десятилетия усилий, что вылилось в теорию движения и сил, которую мы называем Ньютоновской физикой.

Для наших целей самой главной вещью в отношении этих вопросов является то, что они математические. Как сила уменьшается с расстоянием, можно представить, написав простое уравнение. Правильный ответ, который знает любой студент-физик первого года обучения, что сила уменьшается пропорционально квадрату расстояния. Поразительным результатом нашей концепции природы является то, что такое простое математическое соотношение охватывает универсальное явление природы. Природа не должна быть так ошеломляюще проста - и, на самом деле, древние никогда не размышляли о таких простых и универсальных применениях математики для изучения причин движения.

По вопросу о том, как сила вызывает движение, вы должны подумать о движущемся объекте, очерчивающем кривую в пространстве. Тогда вопрос в том, как отличается кривая в зависимости от того, есть ли сила, действующая на объект, или нет. Ответ установлен двумя первыми законами Ньютона. Если силы нет, кривая, вдоль которой движется тело, есть прямая линия. Если сила есть, она вызывает ускорение тела.

Невозможно сформулировать эти законы без математики. Прямая линия суть идеальная математическая концепция; она живет не в нашем мире, а в Платоновом мире идеальных кривых. А что такое ускорение? Это темп изменения скорости, которая сама является темпом изменения положения. Чтобы описать это адекватно, Ньютону пришлось изобрести целый новый раздел математики: дифференциальное исчисление.

Раз у вас есть необходимая математика, она непосредственно вырабатывает следствия. Один из первых вопросов, на который Ньютон должен был дать ответ с помощью своего нового инструментария [6], был о том, какую траекторию будет иметь планета под действием силы от Солнца, которая уменьшается пропорционально квадрату расстояния. Ответ: Это может быть эллипс, парабола или гипербола в зависимости от того, имеет планета замкнутую орбиту или однократно проходит мимо Солнца. Ньютон также сумел обобщить законы падения Галилея в своем законе гравитации [7]. Таким образом, Галилей и Кеплер рассмотрели разные аспекты единого феномена, которым является гравитация.

В истории человеческого разума есть мало чего более глубокого, чем

к оглавлению

открытие этой скрытой общности между падением и движением по орбите. Но под громадностью Ньютоновского достижения имеется непреднамеренное следствие, заключающееся в том, что его труд сделал наше понимание природы намного более математическим, чем ранее. Аристотель и его современники описывали движение в терминах склонностей: Земные объекты имеют склонность стремиться к центру Земли, воздух имеет склонность убегать от центра и так далее. Это была, по существу, описательная наука. Там не было предположений, что пути, вдоль которых двигаются объекты, имеют какие-либо специальные свойства, и, следовательно, не было интереса к использованию математики для описания движения на Земле. Математика, будучи вневременной, была божественной и применимой только к тем божественным и вечным явлениям, которые мы могли видеть и которые были только в небесах.